Building Human Values into Recommender Systems: An Interdisciplinary Synthesis

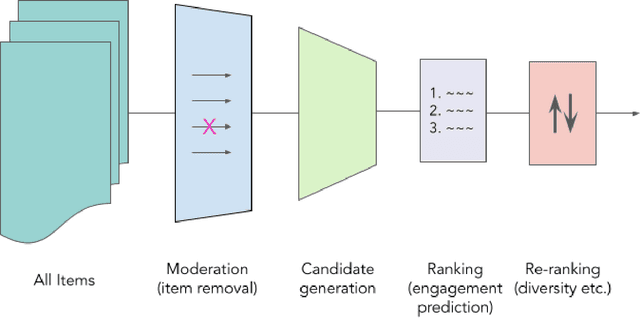
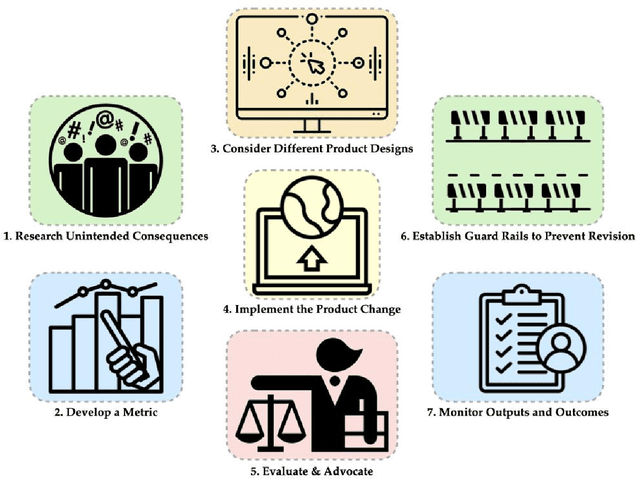
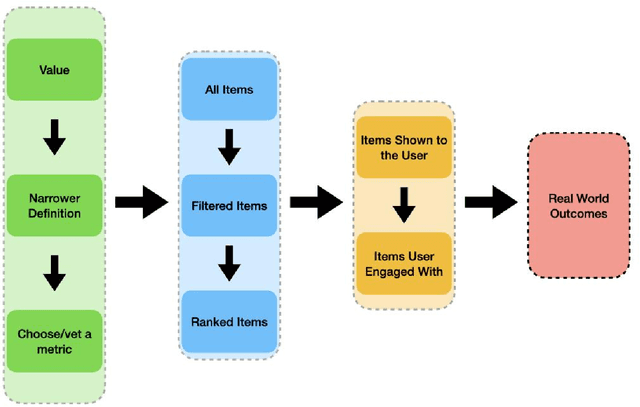
Recommender systems are the algorithms which select, filter, and personalize content across many of the worlds largest platforms and apps. As such, their positive and negative effects on individuals and on societies have been extensively theorized and studied. Our overarching question is how to ensure that recommender systems enact the values of the individuals and societies that they serve. Addressing this question in a principled fashion requires technical knowledge of recommender design and operation, and also critically depends on insights from diverse fields including social science, ethics, economics, psychology, policy and law. This paper is a multidisciplinary effort to synthesize theory and practice from different perspectives, with the goal of providing a shared language, articulating current design approaches, and identifying open problems. It is not a comprehensive survey of this large space, but a set of highlights identified by our diverse author cohort. We collect a set of values that seem most relevant to recommender systems operating across different domains, then examine them from the perspectives of current industry practice, measurement, product design, and policy approaches. Important open problems include multi-stakeholder processes for defining values and resolving trade-offs, better values-driven measurements, recommender controls that people use, non-behavioral algorithmic feedback, optimization for long-term outcomes, causal inference of recommender effects, academic-industry research collaborations, and interdisciplinary policy-making.

Constrained Approximate Maximum Entropy Learning of Markov Random Fields

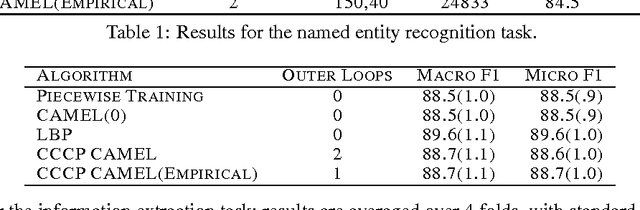
Parameter estimation in Markov random fields (MRFs) is a difficult task, in which inference over the network is run in the inner loop of a gradient descent procedure. Replacing exact inference with approximate methods such as loopy belief propagation (LBP) can suffer from poor convergence. In this paper, we provide a different approach for combining MRF learning and Bethe approximation. We consider the dual of maximum likelihood Markov network learning - maximizing entropy with moment matching constraints - and then approximate both the objective and the constraints in the resulting optimization problem. Unlike previous work along these lines (Teh & Welling, 2003), our formulation allows parameter sharing between features in a general log-linear model, parameter regularization and conditional training. We show that piecewise training (Sutton & McCallum, 2005) is a very restricted special case of this formulation. We study two optimization strategies: one based on a single convex approximation and one that uses repeated convex approximations. We show results on several real-world networks that demonstrate that these algorithms can significantly outperform learning with loopy and piecewise. Our results also provide a framework for analyzing the trade-offs of different relaxations of the entropy objective and of the constraints.