David Kale
Anchored Correlation Explanation: Topic Modeling with Minimal Domain Knowledge
Sep 03, 2018Abstract:While generative models such as Latent Dirichlet Allocation (LDA) have proven fruitful in topic modeling, they often require detailed assumptions and careful specification of hyperparameters. Such model complexity issues only compound when trying to generalize generative models to incorporate human input. We introduce Correlation Explanation (CorEx), an alternative approach to topic modeling that does not assume an underlying generative model, and instead learns maximally informative topics through an information-theoretic framework. This framework naturally generalizes to hierarchical and semi-supervised extensions with no additional modeling assumptions. In particular, word-level domain knowledge can be flexibly incorporated within CorEx through anchor words, allowing topic separability and representation to be promoted with minimal human intervention. Across a variety of datasets, metrics, and experiments, we demonstrate that CorEx produces topics that are comparable in quality to those produced by unsupervised and semi-supervised variants of LDA.
* 21 pages, 7 figures. 2018/09/03: Updated citation for HA/DR dataset
Learning and Optimization with Submodular Functions
May 07, 2015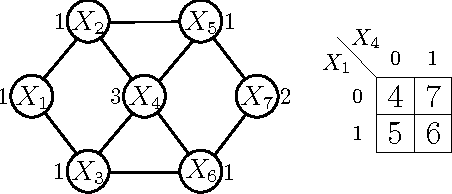
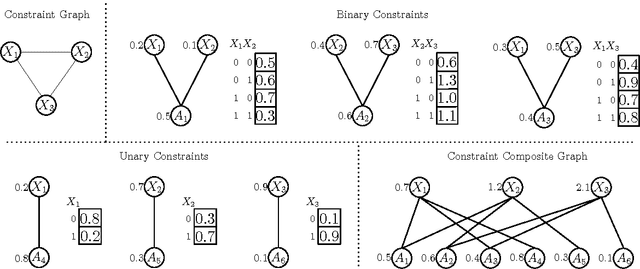
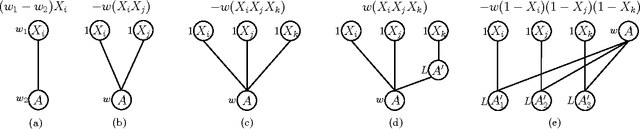
Abstract:In many naturally occurring optimization problems one needs to ensure that the definition of the optimization problem lends itself to solutions that are tractable to compute. In cases where exact solutions cannot be computed tractably, it is beneficial to have strong guarantees on the tractable approximate solutions. In order operate under these criterion most optimization problems are cast under the umbrella of convexity or submodularity. In this report we will study design and optimization over a common class of functions called submodular functions. Set functions, and specifically submodular set functions, characterize a wide variety of naturally occurring optimization problems, and the property of submodularity of set functions has deep theoretical consequences with wide ranging applications. Informally, the property of submodularity of set functions concerns the intuitive "principle of diminishing returns. This property states that adding an element to a smaller set has more value than adding it to a larger set. Common examples of submodular monotone functions are entropies, concave functions of cardinality, and matroid rank functions; non-monotone examples include graph cuts, network flows, and mutual information. In this paper we will review the formal definition of submodularity; the optimization of submodular functions, both maximization and minimization; and finally discuss some applications in relation to learning and reasoning using submodular functions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge