Reducing Data Complexity using Autoencoders with Class-informed Loss Functions

Available data in machine learning applications is becoming increasingly complex, due to higher dimensionality and difficult classes. There exists a wide variety of approaches to measuring complexity of labeled data, according to class overlap, separability or boundary shapes, as well as group morphology. Many techniques can transform the data in order to find better features, but few focus on specifically reducing data complexity. Most data transformation methods mainly treat the dimensionality aspect, leaving aside the available information within class labels which can be useful when classes are somehow complex. This paper proposes an autoencoder-based approach to complexity reduction, using class labels in order to inform the loss function about the adequacy of the generated variables. This leads to three different new feature learners, Scorer, Skaler and Slicer. They are based on Fisher's discriminant ratio, the Kullback-Leibler divergence and least-squares support vector machines, respectively. They can be applied as a preprocessing stage for a binary classification problem. A thorough experimentation across a collection of 27 datasets and a range of complexity and classification metrics shows that class-informed autoencoders perform better than 4 other popular unsupervised feature extraction techniques, especially when the final objective is using the data for a classification task.

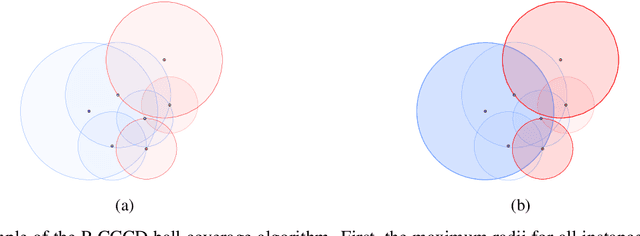
Revisiting Data Complexity Metrics Based on Morphology for Overlap and Imbalance: Snapshot, New Overlap Number of Balls Metrics and Singular Problems Prospect

Data Science and Machine Learning have become fundamental assets for companies and research institutions alike. As one of its fields, supervised classification allows for class prediction of new samples, learning from given training data. However, some properties can cause datasets to be problematic to classify. In order to evaluate a dataset a priori, data complexity metrics have been used extensively. They provide information regarding different intrinsic characteristics of the data, which serve to evaluate classifier compatibility and a course of action that improves performance. However, most complexity metrics focus on just one characteristic of the data, which can be insufficient to properly evaluate the dataset towards the classifiers' performance. In fact, class overlap, a very detrimental feature for the classification process (especially when imbalance among class labels is also present) is hard to assess. This research work focuses on revisiting complexity metrics based on data morphology. In accordance to their nature, the premise is that they provide both good estimates for class overlap, and great correlations with the classification performance. For that purpose, a novel family of metrics have been developed. Being based on ball coverage by classes, they are named after Overlap Number of Balls. Finally, some prospects for the adaptation of the former family of metrics to singular (more complex) problems are discussed.

An analysis on the use of autoencoders for representation learning: fundamentals, learning task case studies, explainability and challenges

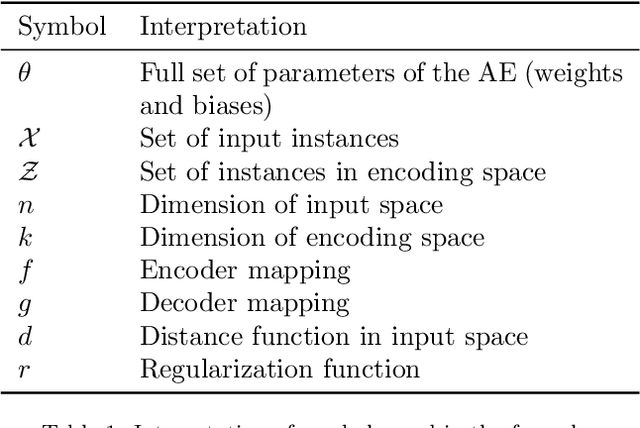
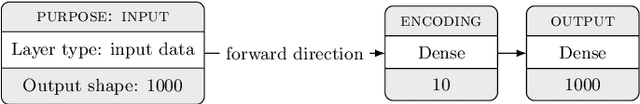
In many machine learning tasks, learning a good representation of the data can be the key to building a well-performant solution. This is because most learning algorithms operate with the features in order to find models for the data. For instance, classification performance can improve if the data is mapped to a space where classes are easily separated, and regression can be facilitated by finding a manifold of data in the feature space. As a general rule, features are transformed by means of statistical methods such as principal component analysis, or manifold learning techniques such as Isomap or locally linear embedding. From a plethora of representation learning methods, one of the most versatile tools is the autoencoder. In this paper we aim to demonstrate how to influence its learned representations to achieve the desired learning behavior. To this end, we present a series of learning tasks: data embedding for visualization, image denoising, semantic hashing, detection of abnormal behaviors and instance generation. We model them from the representation learning perspective, following the state of the art methodologies in each field. A solution is proposed for each task employing autoencoders as the only learning method. The theoretical developments are put into practice using a selection of datasets for the different problems and implementing each solution, followed by a discussion of the results in each case study and a brief explanation of other six learning applications. We also explore the current challenges and approaches to explainability in the context of autoencoders. All of this helps conclude that, thanks to alterations in their structure as well as their objective function, autoencoders may be the core of a possible solution to many problems which can be modeled as a transformation of the feature space.

A Showcase of the Use of Autoencoders in Feature Learning Applications

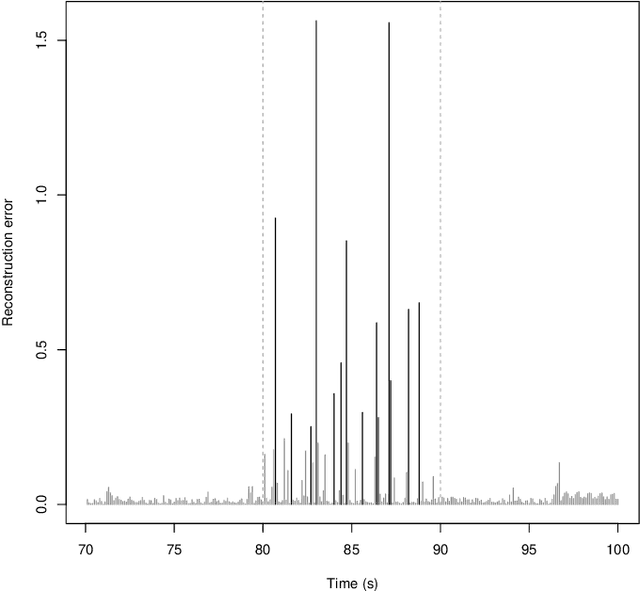
Autoencoders are techniques for data representation learning based on artificial neural networks. Differently to other feature learning methods which may be focused on finding specific transformations of the feature space, they can be adapted to fulfill many purposes, such as data visualization, denoising, anomaly detection and semantic hashing. This work presents these applications and provides details on how autoencoders can perform them, including code samples making use of an R package with an easy-to-use interface for autoencoder design and training, \texttt{ruta}. Along the way, the explanations on how each learning task has been achieved are provided with the aim to help the reader design their own autoencoders for these or other objectives.

A snapshot on nonstandard supervised learning problems: taxonomy, relationships and methods

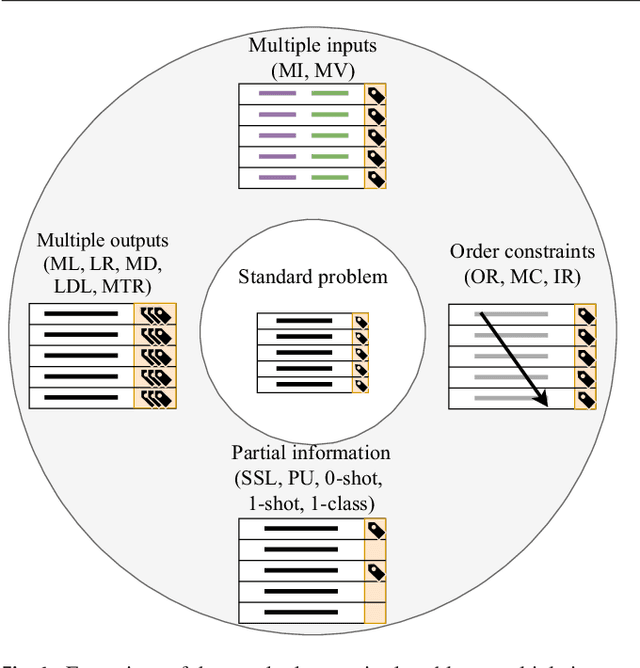
Machine learning is a field which studies how machines can alter and adapt their behavior, improving their actions according to the information they are given. This field is subdivided into multiple areas, among which the best known are supervised learning (e.g. classification and regression) and unsupervised learning (e.g. clustering and association rules). Within supervised learning, most studies and research are focused on well known standard tasks, such as binary classification, multiclass classification and regression with one dependent variable. However, there are many other less known problems. These are what we generically call nonstandard supervised learning problems. The literature about them is much more sparse, and each study is directed to a specific task. Therefore, the definitions, relations and applications of this kind of learners are hard to find. The goal of this paper is to provide the reader with a broad view on the distinct variations of nonstandard supervised problems. A comprehensive taxonomy summarizing their traits is proposed. A review of the common approaches followed to accomplish them and their main applications is provided as well.

Tips, guidelines and tools for managing multi-label datasets: the mldr.datasets R package and the Cometa data repository

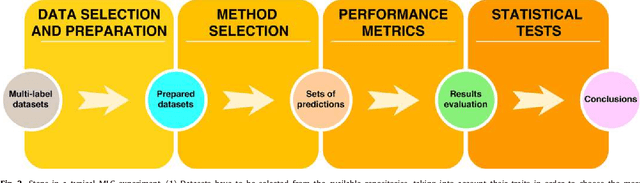
New proposals in the field of multi-label learning algorithms have been growing in number steadily over the last few years. The experimentation associated with each of them always goes through the same phases: selection of datasets, partitioning, training, analysis of results and, finally, comparison with existing methods. This last step is often hampered since it involves using exactly the same datasets, partitioned in the same way and using the same validation strategy. In this paper we present a set of tools whose objective is to facilitate the management of multi-label datasets, aiming to standardize the experimentation procedure. The two main tools are an R package, mldr.datasets, and a web repository with datasets, Cometa. Together, these tools will simplify the collection of datasets, their partitioning, documentation and export to multiple formats, among other functions. Some tips, recommendations and guidelines for a good experimental analysis of multi-label methods are also presented.

A practical tutorial on autoencoders for nonlinear feature fusion: Taxonomy, models, software and guidelines

Many of the existing machine learning algorithms, both supervised and unsupervised, depend on the quality of the input characteristics to generate a good model. The amount of these variables is also important, since performance tends to decline as the input dimensionality increases, hence the interest in using feature fusion techniques, able to produce feature sets that are more compact and higher level. A plethora of procedures to fuse original variables for producing new ones has been developed in the past decades. The most basic ones use linear combinations of the original variables, such as PCA (Principal Component Analysis) and LDA (Linear Discriminant Analysis), while others find manifold embeddings of lower dimensionality based on non-linear combinations, such as Isomap or LLE (Linear Locally Embedding) techniques. More recently, autoencoders (AEs) have emerged as an alternative to manifold learning for conducting nonlinear feature fusion. Dozens of AE models have been proposed lately, each with its own specific traits. Although many of them can be used to generate reduced feature sets through the fusion of the original ones, there also AEs designed with other applications in mind. The goal of this paper is to provide the reader with a broad view of what an AE is, how they are used for feature fusion, a taxonomy gathering a broad range of models, and how they relate to other classical techniques. In addition, a set of didactic guidelines on how to choose the proper AE for a given task is supplied, together with a discussion of the software tools available. Finally, two case studies illustrate the usage of AEs with datasets of handwritten digits and breast cancer.