Fair Overlap Number of Balls (Fair-ONB): A Data-Morphology-based Undersampling Method for Bias Reduction

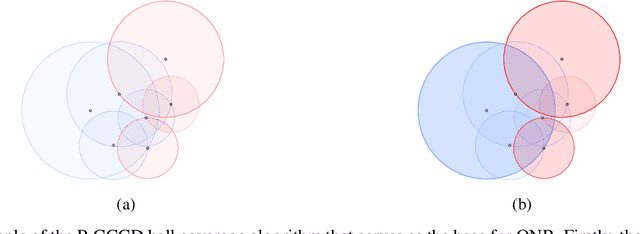
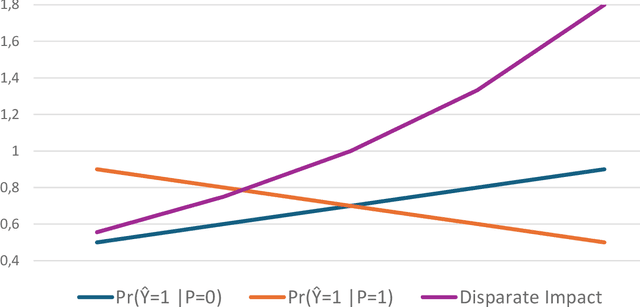
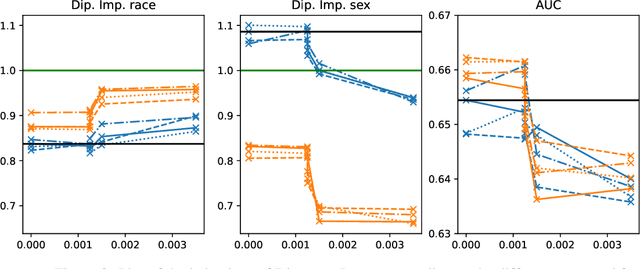
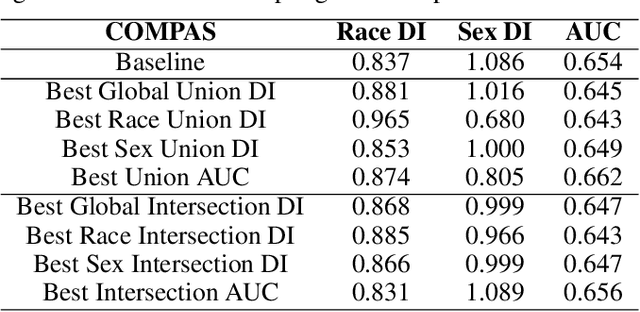
Given the magnitude of data generation currently, both in quantity and speed, the use of machine learning is increasingly important. When data include protected features that might give rise to discrimination, special care must be taken. Data quality is critical in these cases, as biases in training data can be reflected in classification models. This has devastating consequences and fails to comply with current regulations. Data-Centric Artificial Intelligence proposes dataset modifications to improve its quality. Instance selection via undersampling can foster balanced learning of classes and protected feature values in the classifier. When such undersampling is done close to the decision boundary, the effect on the classifier would be bolstered. This work proposes Fair Overlap Number of Balls (Fair-ONB), an undersampling method that harnesses the data morphology of the different data groups (obtained from the combination of classes and protected feature values) to perform guided undersampling in the areas where they overlap. It employs attributes of the ball coverage of the groups, such as the radius, number of covered instances and density, to select the most suitable areas for undersampling and reduce bias. Results show that the Fair-ONB method reduces bias with low impact on the classifier's predictive performance.

Overlap Number of Balls Model-Agnostic CounterFactuals (ONB-MACF): A Data-Morphology-based Counterfactual Generation Method for Trustworthy Artificial Intelligence

Explainable Artificial Intelligence (XAI) is a pivotal research domain aimed at understanding the operational mechanisms of AI systems, particularly those considered ``black boxes'' due to their complex, opaque nature. XAI seeks to make these AI systems more understandable and trustworthy, providing insight into their decision-making processes. By producing clear and comprehensible explanations, XAI enables users, practitioners, and stakeholders to trust a model's decisions. This work analyses the value of data morphology strategies in generating counterfactual explanations. It introduces the Overlap Number of Balls Model-Agnostic CounterFactuals (ONB-MACF) method, a model-agnostic counterfactual generator that leverages data morphology to estimate a model's decision boundaries. The ONB-MACF method constructs hyperspheres in the data space whose covered points share a class, mapping the decision boundary. Counterfactuals are then generated by incrementally adjusting an instance's attributes towards the nearest alternate-class hypersphere, crossing the decision boundary with minimal modifications. By design, the ONB-MACF method generates feasible and sparse counterfactuals that follow the data distribution. Our comprehensive benchmark from a double perspective (quantitative and qualitative) shows that the ONB-MACF method outperforms existing state-of-the-art counterfactual generation methods across multiple quality metrics on diverse tabular datasets. This supports our hypothesis, showcasing the potential of data-morphology-based explainability strategies for trustworthy AI.

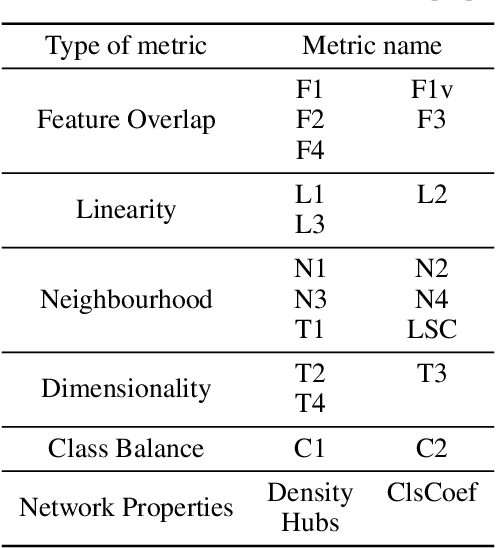
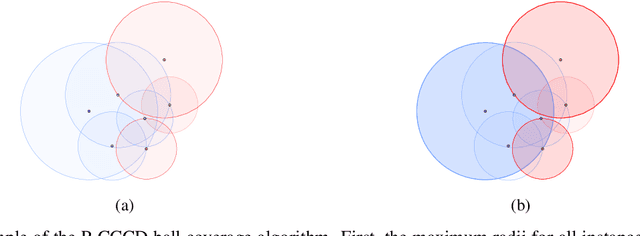
Revisiting Data Complexity Metrics Based on Morphology for Overlap and Imbalance: Snapshot, New Overlap Number of Balls Metrics and Singular Problems Prospect

Data Science and Machine Learning have become fundamental assets for companies and research institutions alike. As one of its fields, supervised classification allows for class prediction of new samples, learning from given training data. However, some properties can cause datasets to be problematic to classify. In order to evaluate a dataset a priori, data complexity metrics have been used extensively. They provide information regarding different intrinsic characteristics of the data, which serve to evaluate classifier compatibility and a course of action that improves performance. However, most complexity metrics focus on just one characteristic of the data, which can be insufficient to properly evaluate the dataset towards the classifiers' performance. In fact, class overlap, a very detrimental feature for the classification process (especially when imbalance among class labels is also present) is hard to assess. This research work focuses on revisiting complexity metrics based on data morphology. In accordance to their nature, the premise is that they provide both good estimates for class overlap, and great correlations with the classification performance. For that purpose, a novel family of metrics have been developed. Being based on ball coverage by classes, they are named after Overlap Number of Balls. Finally, some prospects for the adaptation of the former family of metrics to singular (more complex) problems are discussed.