SciSciGPT: Advancing Human-AI Collaboration in the Science of Science

The increasing availability of large-scale datasets has fueled rapid progress across many scientific fields, creating unprecedented opportunities for research and discovery while posing significant analytical challenges. Recent advances in large language models (LLMs) and AI agents have opened new possibilities for human-AI collaboration, offering powerful tools to navigate this complex research landscape. In this paper, we introduce SciSciGPT, an open-source, prototype AI collaborator that uses the science of science as a testbed to explore the potential of LLM-powered research tools. SciSciGPT automates complex workflows, supports diverse analytical approaches, accelerates research prototyping and iteration, and facilitates reproducibility. Through case studies, we demonstrate its ability to streamline a wide range of empirical and analytical research tasks while highlighting its broader potential to advance research. We further propose an LLM Agent capability maturity model for human-AI collaboration, envisioning a roadmap to further improve and expand upon frameworks like SciSciGPT. As AI capabilities continue to evolve, frameworks like SciSciGPT may play increasingly pivotal roles in scientific research and discovery, unlocking further opportunities. At the same time, these new advances also raise critical challenges, from ensuring transparency and ethical use to balancing human and AI contributions. Addressing these issues may shape the future of scientific inquiry and inform how we train the next generation of scientists to thrive in an increasingly AI-integrated research ecosystem.

Quantifying the Benefit of Artificial Intelligence for Scientific Research

The ongoing artificial intelligence (AI) revolution has the potential to change almost every line of work. As AI capabilities continue to improve in accuracy, robustness, and reach, AI may outperform and even replace human experts across many valuable tasks. Despite enormous efforts devoted to understanding AI's impact on labor and the economy and its recent success in accelerating scientific discovery and progress, we lack a systematic understanding of how advances in AI may benefit scientific research across disciplines and fields. Here we develop a measurement framework to estimate both the direct use of AI and the potential benefit of AI in scientific research by applying natural language processing techniques to 87.6 million publications and 7.1 million patents. We find that the use of AI in research appears widespread throughout the sciences, growing especially rapidly since 2015, and papers that use AI exhibit an impact premium, more likely to be highly cited both within and outside their disciplines. While almost every discipline contains some subfields that benefit substantially from AI, analyzing 4.6 million course syllabi across various educational disciplines, we find a systematic misalignment between the education of AI and its impact on research, suggesting the supply of AI talents in scientific disciplines is not commensurate with AI research demands. Lastly, examining who benefits from AI within the scientific workforce, we find that disciplines with a higher proportion of women or black scientists tend to be associated with less benefit, suggesting that AI's growing impact on research may further exacerbate existing inequalities in science. As the connection between AI and scientific research deepens, our findings may have an increasing value, with important implications for the equity and sustainability of the research enterprise.

Automatic Symmetry Discovery with Lie Algebra Convolutional Network

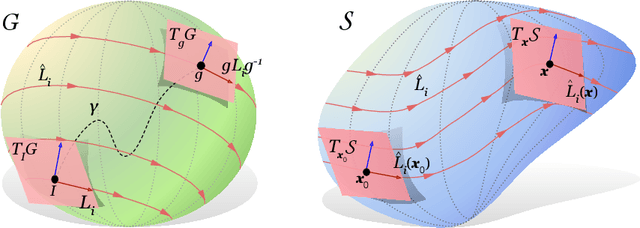
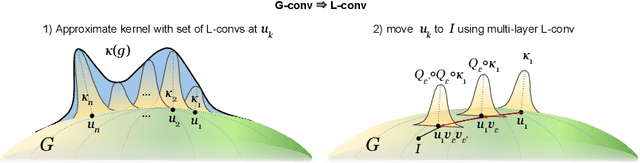
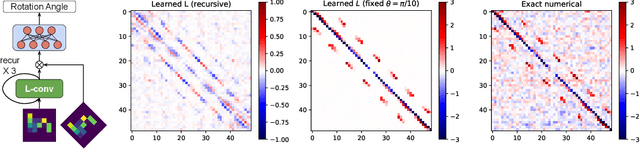
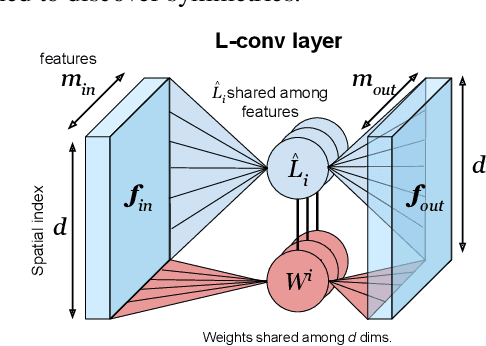
Existing equivariant neural networks for continuous groups require discretization or group representations. All these approaches require detailed knowledge of the group parametrization and cannot learn entirely new symmetries. We propose to work with the Lie algebra (infinitesimal generators) instead of the Lie group.Our model, the Lie algebra convolutional network (L-conv) can learn potential symmetries and does not require discretization of the group. We show that L-conv can serve as a building block to construct any group equivariant architecture. We discuss how CNNs and Graph Convolutional Networks are related to and can be expressed as L-conv with appropriate groups. We also derive the MSE loss for a single L-conv layer and find a deep relation with Lagrangians used in physics, with some of the physics aiding in defining generalization and symmetries in the loss landscape. Conversely, L-conv could be used to propose more general equivariant ans\"atze for scientific machine learning.