Reproducing sensory induced hallucinations via neural fields

Understanding sensory-induced cortical patterns in the primary visual cortex V1 is an important challenge both for physiological motivations and for improving our understanding of human perception and visual organisation. In this work, we focus on pattern formation in the visual cortex when the cortical activity is driven by a geometric visual hallucination-like stimulus. In particular, we present a theoretical framework for sensory-induced hallucinations which allows one to reproduce novel psychophysical results such as the MacKay effect (Nature, 1957) and the Billock and Tsou experiences (PNAS, 2007).

An auditory cortex model for sound processing

The reconstruction mechanisms built by the human auditory system during sound reconstruction are still a matter of debate. The purpose of this study is to refine the auditory cortex model introduced in [9], and inspired by the geometrical modelling of vision. The algorithm transforms the degraded sound in an 'image' in the time-frequency domain via a short-time Fourier transform. Such an image is then lifted in the Heisenberg group and it is reconstructed via a Wilson-Cowan differo-integral equation. Numerical experiments on a library of speech recordings are provided, showing the good reconstruction properties of the algorithm.

A cortical-inspired sub-Riemannian model for Poggendorff-type visual illusions

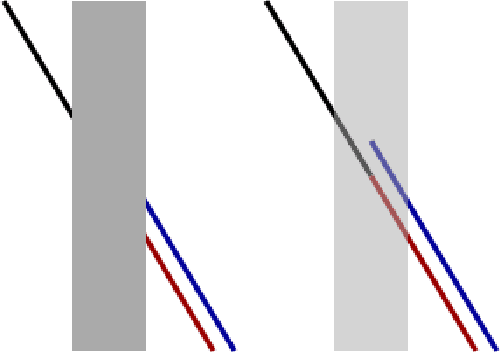
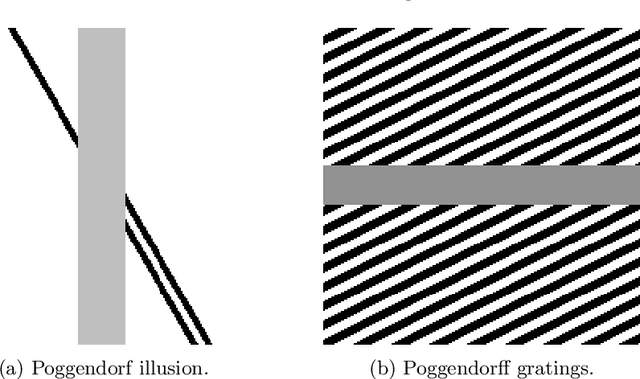
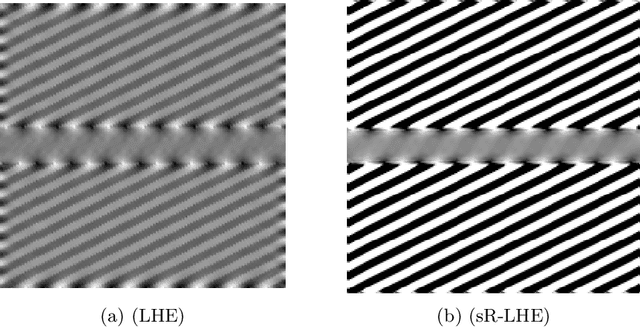
We consider Wilson-Cowan-type models for the mathematical description of orientation-dependent Poggendorff-like illusions. Our modelling improves two previously proposed cortical-inspired approaches embedding the sub-Riemannian heat kernel into the neuronal interaction term, in agreement with the intrinsically anisotropic functional architecture of V1 based on both local and lateral connections. For the numerical realisation of both models, we consider standard gradient descent algorithms combined with Fourier-based approaches for the efficient computation of the sub-Laplacian evolution. Our numerical results show that the use of the sub-Riemannian kernel allows to reproduce numerically visual misperceptions and inpainting-type biases in a stronger way in comparison with the previous approaches.

Cortical-inspired Wilson-Cowan-type equations for orientation-dependent contrast perception modelling

We consider the evolution model proposed in [9, 6] to describe illusory contrast perception phenomena induced by surrounding orientations. Firstly, we highlight its analogies and differences with widely used Wilson-Cowan equations [48], mainly in terms of efficient representation properties. Then, in order to explicitly encode local directional information, we exploit the model of the primary visual cortex V1 proposed in [20] and largely used over the last years for several image processing problems [24,38,28]. The resulting model is capable to describe assimilation and contrast visual bias at the same time, the main novelty being its explicit dependence on local image orientation. We report several numerical tests showing the ability of the model to explain, in particular, orientation-dependent phenomena such as grating induction and a modified version of the Poggendorff illusion. For this latter example, we empirically show the existence of a set of threshold parameters differentiating from inpainting to perception-type reconstructions, describing long-range connectivity between different hypercolumns in the primary visual cortex.

A cortical-inspired model for orientation-dependent contrast perception: a link with Wilson-Cowan equations

We consider a differential model describing neuro-physiological contrast perception phenomena induced by surrounding orientations. The mathematical formulation relies on a cortical-inspired modelling [10] largely used over the last years to describe neuron interactions in the primary visual cortex (V1) and applied to several image processing problems [12,19,13]. Our model connects to Wilson-Cowan-type equations [23] and it is analogous to the one used in [3,2,14] to describe assimilation and contrast phenomena, the main novelty being its explicit dependence on local image orientation. To confirm the validity of the model, we report some numerical tests showing its ability to explain orientation-dependent phenomena (such as grating induction) and geometric-optical illusions [21,16] classically explained only by filtering-based techniques [6,18].

Highly corrupted image inpainting through hypoelliptic diffusion

We present a new image inpainting algorithm, the Averaging and Hypoelliptic Evolution (AHE) algorithm, inspired by the one presented in [SIAM J. Imaging Sci., vol. 7, no. 2, pp. 669--695, 2014] and based upon a semi-discrete variation of the Citti-Petitot-Sarti model of the primary visual cortex V1. The AHE algorithm is based on a suitable combination of sub-Riemannian hypoelliptic diffusion and ad-hoc local averaging techniques. In particular, we focus on reconstructing highly corrupted images (i.e. where more than the 80% of the image is missing), for which we obtain reconstructions comparable with the state-of-the-art.

Cortical-inspired image reconstruction via sub-Riemannian geometry and hypoelliptic diffusion

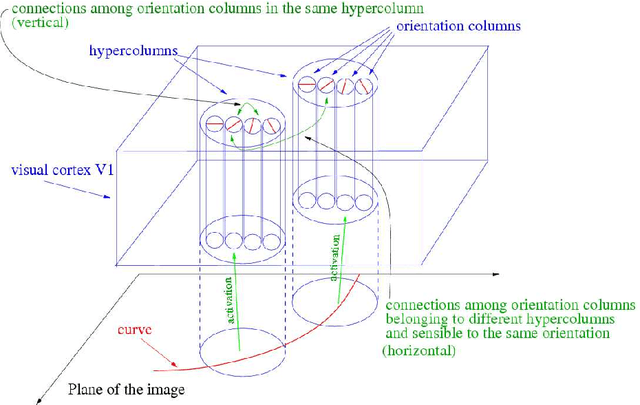
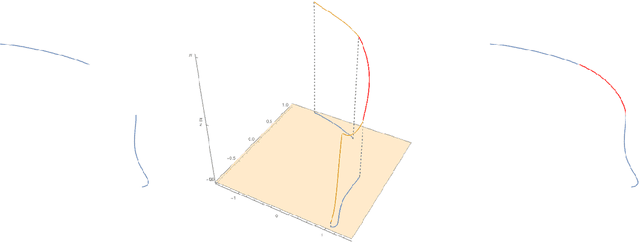
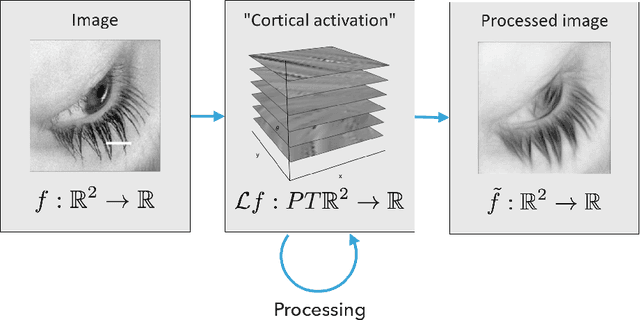
In this paper we review several algorithms for image inpainting based on the hypoelliptic diffusion naturally associated with a mathematical model of the primary visual cortex. In particular, we present one algorithm that does not exploit the information of where the image is corrupted, and others that do it. While the first algorithm is able to reconstruct only images that our visual system is still capable of recognize, we show that those of the second type completely transcend such limitation providing reconstructions at the state-of-the-art in image inpainting. This can be interpreted as a validation of the fact that our visual cortex actually encodes the first type of algorithm.

A semidiscrete version of the Citti-Petitot-Sarti model as a plausible model for anthropomorphic image reconstruction and pattern recognition

In his beautiful book [66], Jean Petitot proposes a sub-Riemannian model for the primary visual cortex of mammals. This model is neurophysiologically justified. Further developments of this theory lead to efficient algorithms for image reconstruction, based upon the consideration of an associated hypoelliptic diffusion. The sub-Riemannian model of Petitot and Citti-Sarti (or certain of its improvements) is a left-invariant structure over the group $SE(2)$ of rototranslations of the plane. Here, we propose a semi-discrete version of this theory, leading to a left-invariant structure over the group $SE(2,N)$, restricting to a finite number of rotations. This apparently very simple group is in fact quite atypical: it is maximally almost periodic, which leads to much simpler harmonic analysis compared to $SE(2).$ Based upon this semi-discrete model, we improve on previous image-reconstruction algorithms and we develop a pattern-recognition theory that leads also to very efficient algorithms in practice.

Generalized Fourier-Bessel operator and almost-periodic interpolation and approximation

We consider functions $f$ of two real variables, given as trigonometric functions over a finite set $F$ of frequencies. This set is assumed to be closed under rotations in the frequency plane of angle $\frac{2k\pi}{M}$ for some integer $M$. Firstly, we address the problem of evaluating these functions over a similar finite set $E$ in the space plane and, secondly, we address the problems of interpolating or approximating a function $g$ of two variables by such an $f$ over the grid $E.$ In particular, for this aim, we establish an abstract factorization theorem for the evaluation function, which is a key point for an efficient numerical solution to these problems. This result is based on the very special structure of the group $SE(2,N)$, subgroup of the group $SE(2)$ of motions of the plane corresponding to discrete rotations, which is a maximally almost periodic group. Although the motivation of this paper comes from our previous works on biomimetic image reconstruction and pattern recognition, where these questions appear naturally, this topic is related with several classical problems: the FFT in polar coordinates, the Non Uniform FFT, the evaluation of general trigonometric polynomials, and so on.

Fourier descriptors based on the structure of the human primary visual cortex with applications to object recognition

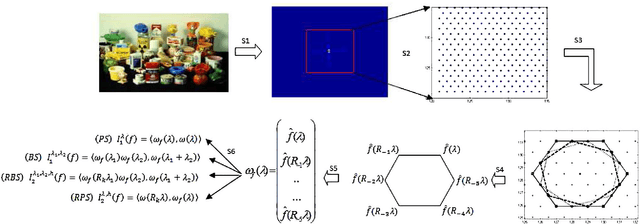
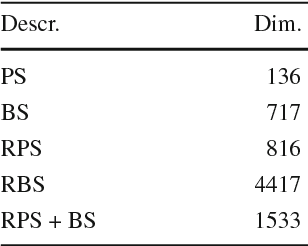
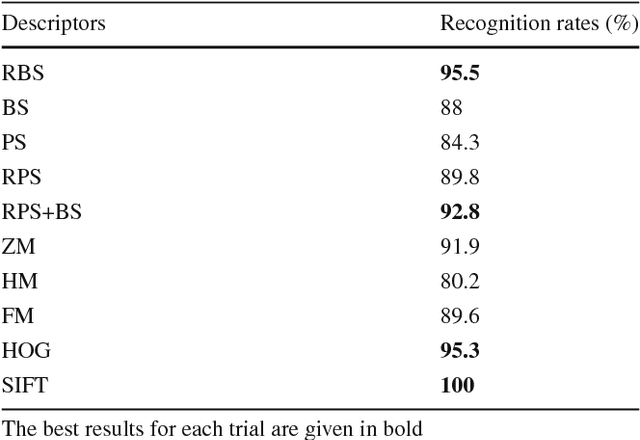
In this paper we propose a supervised object recognition method using new global features and inspired by the model of the human primary visual cortex V1 as the semidiscrete roto-translation group $SE(2,N) = \mathbb Z_N\rtimes \mathbb R^2$. The proposed technique is based on generalized Fourier descriptors on the latter group, which are invariant to natural geometric transformations (rotations, translations). These descriptors are then used to feed an SVM classifier. We have tested our method against the COIL-100 image database and the ORL face database, and compared it with other techniques based on traditional descriptors, global and local. The obtained results have shown that our approach looks extremely efficient and stable to noise, in presence of which it outperforms the other techniques analyzed in the paper.