A cortical-inspired sub-Riemannian model for Poggendorff-type visual illusions

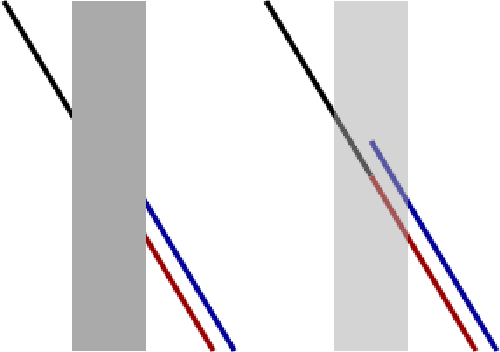
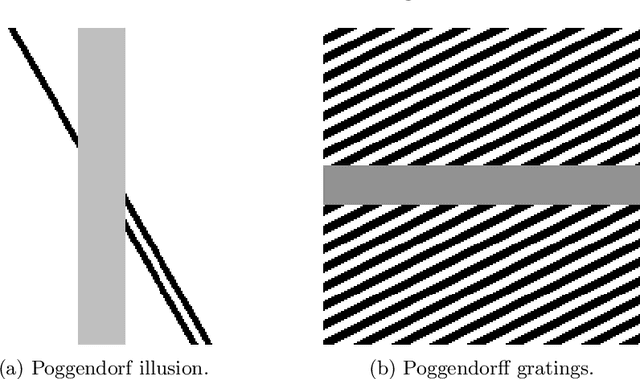
We consider Wilson-Cowan-type models for the mathematical description of orientation-dependent Poggendorff-like illusions. Our modelling improves two previously proposed cortical-inspired approaches embedding the sub-Riemannian heat kernel into the neuronal interaction term, in agreement with the intrinsically anisotropic functional architecture of V1 based on both local and lateral connections. For the numerical realisation of both models, we consider standard gradient descent algorithms combined with Fourier-based approaches for the efficient computation of the sub-Laplacian evolution. Our numerical results show that the use of the sub-Riemannian kernel allows to reproduce numerically visual misperceptions and inpainting-type biases in a stronger way in comparison with the previous approaches.

Cortical-inspired Wilson-Cowan-type equations for orientation-dependent contrast perception modelling

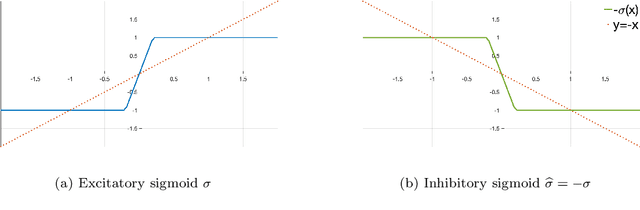
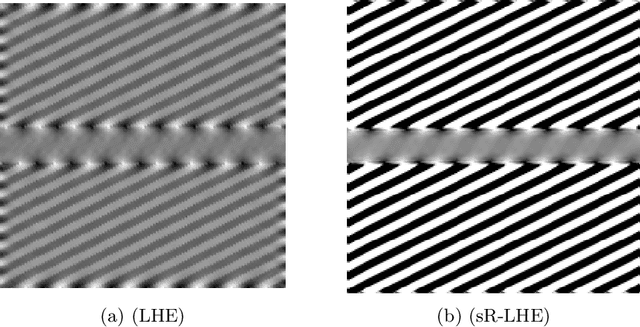
We consider the evolution model proposed in [9, 6] to describe illusory contrast perception phenomena induced by surrounding orientations. Firstly, we highlight its analogies and differences with widely used Wilson-Cowan equations [48], mainly in terms of efficient representation properties. Then, in order to explicitly encode local directional information, we exploit the model of the primary visual cortex V1 proposed in [20] and largely used over the last years for several image processing problems [24,38,28]. The resulting model is capable to describe assimilation and contrast visual bias at the same time, the main novelty being its explicit dependence on local image orientation. We report several numerical tests showing the ability of the model to explain, in particular, orientation-dependent phenomena such as grating induction and a modified version of the Poggendorff illusion. For this latter example, we empirically show the existence of a set of threshold parameters differentiating from inpainting to perception-type reconstructions, describing long-range connectivity between different hypercolumns in the primary visual cortex.

A cortical-inspired model for orientation-dependent contrast perception: a link with Wilson-Cowan equations

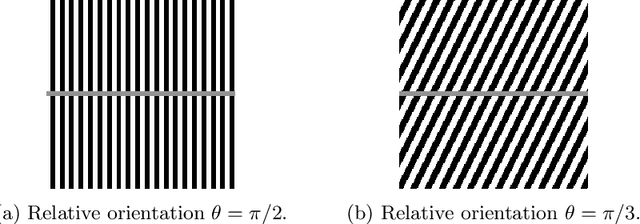
We consider a differential model describing neuro-physiological contrast perception phenomena induced by surrounding orientations. The mathematical formulation relies on a cortical-inspired modelling [10] largely used over the last years to describe neuron interactions in the primary visual cortex (V1) and applied to several image processing problems [12,19,13]. Our model connects to Wilson-Cowan-type equations [23] and it is analogous to the one used in [3,2,14] to describe assimilation and contrast phenomena, the main novelty being its explicit dependence on local image orientation. To confirm the validity of the model, we report some numerical tests showing its ability to explain orientation-dependent phenomena (such as grating induction) and geometric-optical illusions [21,16] classically explained only by filtering-based techniques [6,18].