Multi-frequency image completion via a biologically-inspired sub-Riemannian model with frequency and phase

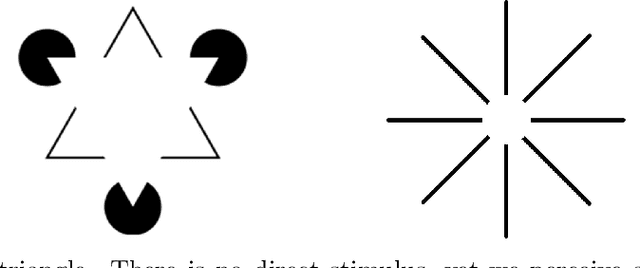
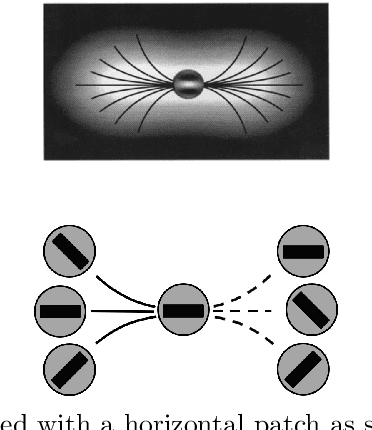
We present a novel cortically-inspired image completion algorithm. It uses a five dimensional sub-Riemannian cortical geometry modelling the orientation, spatial frequency and phase selective behavior of the cells in the visual cortex. The algorithm extracts the orientation, frequency and phase information existing in a given two dimensional corrupted input image via a Gabor transform and represent those values in terms of cortical cell output responses in the model geometry. Then it performs completion via a diffusion concentrated in a neighbourhood along the neural connections within the model geometry. The diffusion models the activity propagation integrating orientation, frequency and phase features along the neural connections. Finally, the algorithm transforms back the diffused and completed output responses back to the two dimensional image plane.

A cortical-inspired sub-Riemannian model for Poggendorff-type visual illusions

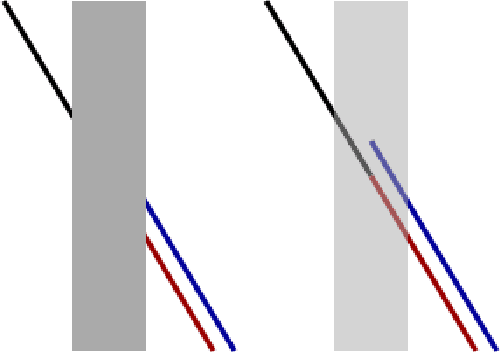
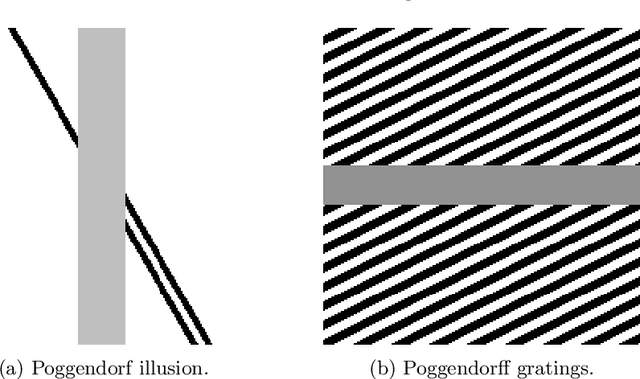
We consider Wilson-Cowan-type models for the mathematical description of orientation-dependent Poggendorff-like illusions. Our modelling improves two previously proposed cortical-inspired approaches embedding the sub-Riemannian heat kernel into the neuronal interaction term, in agreement with the intrinsically anisotropic functional architecture of V1 based on both local and lateral connections. For the numerical realisation of both models, we consider standard gradient descent algorithms combined with Fourier-based approaches for the efficient computation of the sub-Laplacian evolution. Our numerical results show that the use of the sub-Riemannian kernel allows to reproduce numerically visual misperceptions and inpainting-type biases in a stronger way in comparison with the previous approaches.