A cortical-inspired sub-Riemannian model for Poggendorff-type visual illusions

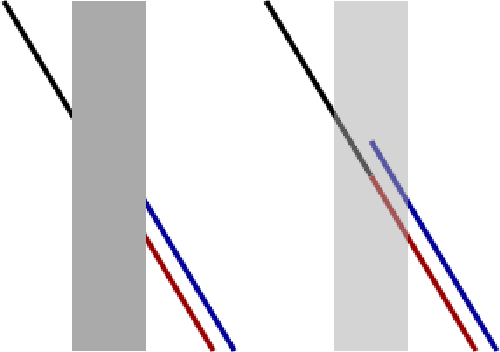
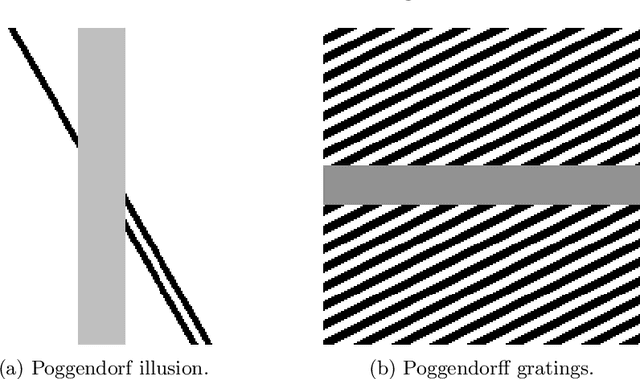
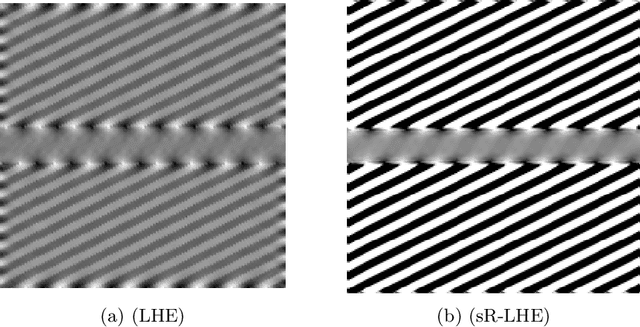
We consider Wilson-Cowan-type models for the mathematical description of orientation-dependent Poggendorff-like illusions. Our modelling improves two previously proposed cortical-inspired approaches embedding the sub-Riemannian heat kernel into the neuronal interaction term, in agreement with the intrinsically anisotropic functional architecture of V1 based on both local and lateral connections. For the numerical realisation of both models, we consider standard gradient descent algorithms combined with Fourier-based approaches for the efficient computation of the sub-Laplacian evolution. Our numerical results show that the use of the sub-Riemannian kernel allows to reproduce numerically visual misperceptions and inpainting-type biases in a stronger way in comparison with the previous approaches.