Highly corrupted image inpainting through hypoelliptic diffusion

We present a new image inpainting algorithm, the Averaging and Hypoelliptic Evolution (AHE) algorithm, inspired by the one presented in [SIAM J. Imaging Sci., vol. 7, no. 2, pp. 669--695, 2014] and based upon a semi-discrete variation of the Citti-Petitot-Sarti model of the primary visual cortex V1. The AHE algorithm is based on a suitable combination of sub-Riemannian hypoelliptic diffusion and ad-hoc local averaging techniques. In particular, we focus on reconstructing highly corrupted images (i.e. where more than the 80% of the image is missing), for which we obtain reconstructions comparable with the state-of-the-art.

Cortical-inspired image reconstruction via sub-Riemannian geometry and hypoelliptic diffusion

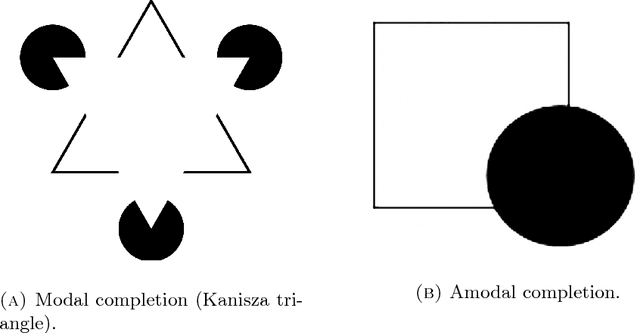
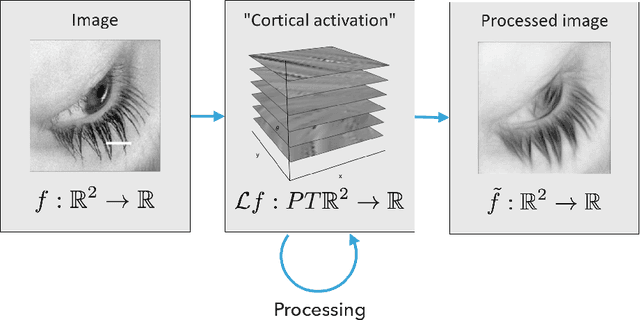
In this paper we review several algorithms for image inpainting based on the hypoelliptic diffusion naturally associated with a mathematical model of the primary visual cortex. In particular, we present one algorithm that does not exploit the information of where the image is corrupted, and others that do it. While the first algorithm is able to reconstruct only images that our visual system is still capable of recognize, we show that those of the second type completely transcend such limitation providing reconstructions at the state-of-the-art in image inpainting. This can be interpreted as a validation of the fact that our visual cortex actually encodes the first type of algorithm.

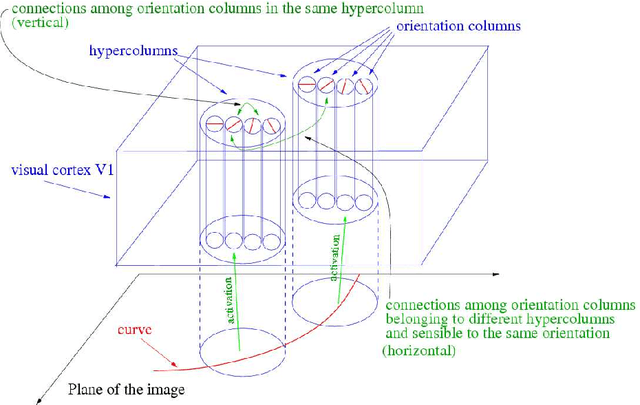
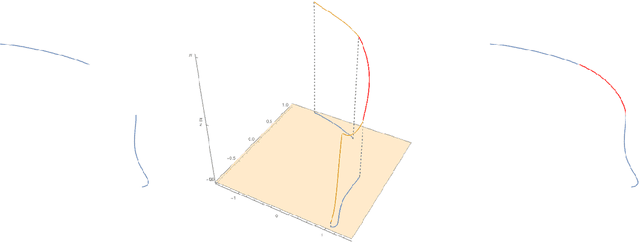
A semidiscrete version of the Citti-Petitot-Sarti model as a plausible model for anthropomorphic image reconstruction and pattern recognition

In his beautiful book [66], Jean Petitot proposes a sub-Riemannian model for the primary visual cortex of mammals. This model is neurophysiologically justified. Further developments of this theory lead to efficient algorithms for image reconstruction, based upon the consideration of an associated hypoelliptic diffusion. The sub-Riemannian model of Petitot and Citti-Sarti (or certain of its improvements) is a left-invariant structure over the group $SE(2)$ of rototranslations of the plane. Here, we propose a semi-discrete version of this theory, leading to a left-invariant structure over the group $SE(2,N)$, restricting to a finite number of rotations. This apparently very simple group is in fact quite atypical: it is maximally almost periodic, which leads to much simpler harmonic analysis compared to $SE(2).$ Based upon this semi-discrete model, we improve on previous image-reconstruction algorithms and we develop a pattern-recognition theory that leads also to very efficient algorithms in practice.

Generalized Fourier-Bessel operator and almost-periodic interpolation and approximation

We consider functions $f$ of two real variables, given as trigonometric functions over a finite set $F$ of frequencies. This set is assumed to be closed under rotations in the frequency plane of angle $\frac{2k\pi}{M}$ for some integer $M$. Firstly, we address the problem of evaluating these functions over a similar finite set $E$ in the space plane and, secondly, we address the problems of interpolating or approximating a function $g$ of two variables by such an $f$ over the grid $E.$ In particular, for this aim, we establish an abstract factorization theorem for the evaluation function, which is a key point for an efficient numerical solution to these problems. This result is based on the very special structure of the group $SE(2,N)$, subgroup of the group $SE(2)$ of motions of the plane corresponding to discrete rotations, which is a maximally almost periodic group. Although the motivation of this paper comes from our previous works on biomimetic image reconstruction and pattern recognition, where these questions appear naturally, this topic is related with several classical problems: the FFT in polar coordinates, the Non Uniform FFT, the evaluation of general trigonometric polynomials, and so on.

Fourier descriptors based on the structure of the human primary visual cortex with applications to object recognition

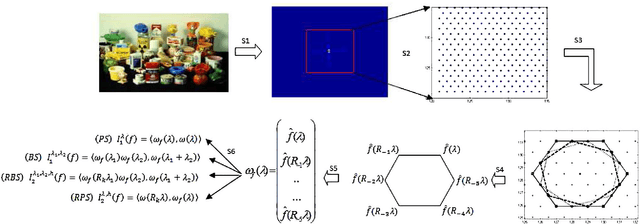
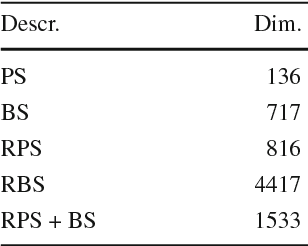
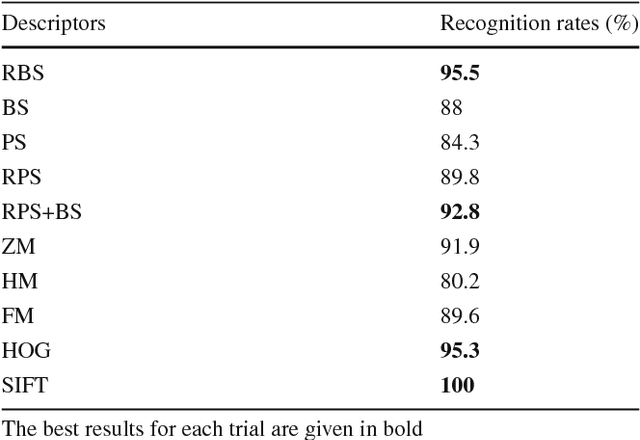
In this paper we propose a supervised object recognition method using new global features and inspired by the model of the human primary visual cortex V1 as the semidiscrete roto-translation group $SE(2,N) = \mathbb Z_N\rtimes \mathbb R^2$. The proposed technique is based on generalized Fourier descriptors on the latter group, which are invariant to natural geometric transformations (rotations, translations). These descriptors are then used to feed an SVM classifier. We have tested our method against the COIL-100 image database and the ORL face database, and compared it with other techniques based on traditional descriptors, global and local. The obtained results have shown that our approach looks extremely efficient and stable to noise, in presence of which it outperforms the other techniques analyzed in the paper.