Simple Multigraph Convolution Networks

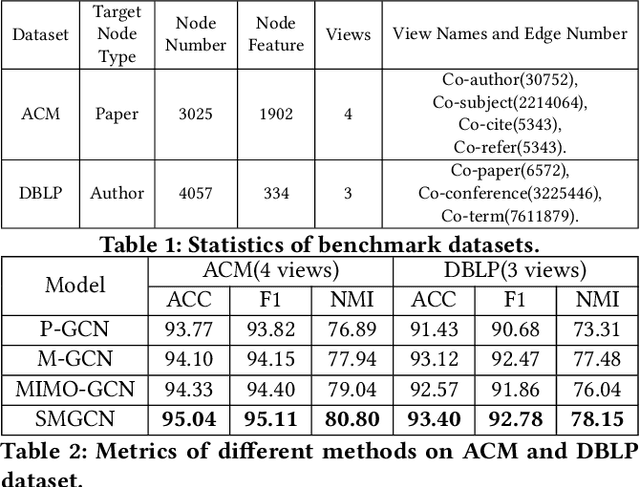
Existing multigraph convolution methods either ignore the cross-view interaction among multiple graphs, or induce extremely high computational cost due to standard cross-view polynomial operators. To alleviate this problem, this paper proposes a Simple MultiGraph Convolution Networks (SMGCN) which first extracts consistent cross-view topology from multigraphs including edge-level and subgraph-level topology, then performs polynomial expansion based on raw multigraphs and consistent topologies. In theory, SMGCN utilizes the consistent topologies in polynomial expansion rather than standard cross-view polynomial expansion, which performs credible cross-view spatial message-passing, follows the spectral convolution paradigm, and effectively reduces the complexity of standard polynomial expansion. In the simulations, experimental results demonstrate that SMGCN achieves state-of-the-art performance on ACM and DBLP multigraph benchmark datasets. Our codes are available at https://github.com/frinkleko/SMGCN.

A Novel Normalized-Cut Solver with Nearest Neighbor Hierarchical Initialization

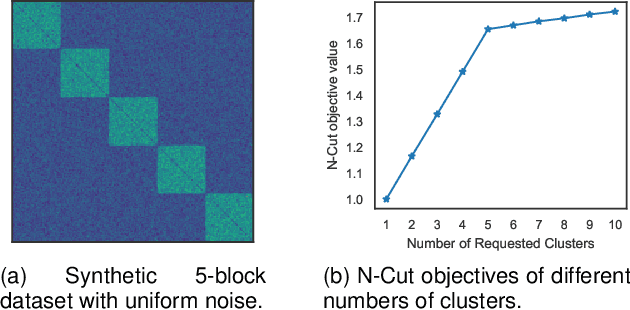
Normalized-Cut (N-Cut) is a famous model of spectral clustering. The traditional N-Cut solvers are two-stage: 1) calculating the continuous spectral embedding of normalized Laplacian matrix; 2) discretization via $K$-means or spectral rotation. However, this paradigm brings two vital problems: 1) two-stage methods solve a relaxed version of the original problem, so they cannot obtain good solutions for the original N-Cut problem; 2) solving the relaxed problem requires eigenvalue decomposition, which has $\mathcal{O}(n^3)$ time complexity ($n$ is the number of nodes). To address the problems, we propose a novel N-Cut solver designed based on the famous coordinate descent method. Since the vanilla coordinate descent method also has $\mathcal{O}(n^3)$ time complexity, we design various accelerating strategies to reduce the time complexity to $\mathcal{O}(|E|)$ ($|E|$ is the number of edges). To avoid reliance on random initialization which brings uncertainties to clustering, we propose an efficient initialization method that gives deterministic outputs. Extensive experiments on several benchmark datasets demonstrate that the proposed solver can obtain larger objective values of N-Cut, meanwhile achieving better clustering performance compared to traditional solvers.

NP$^2$L: Negative Pseudo Partial Labels Extraction for Graph Neural Networks

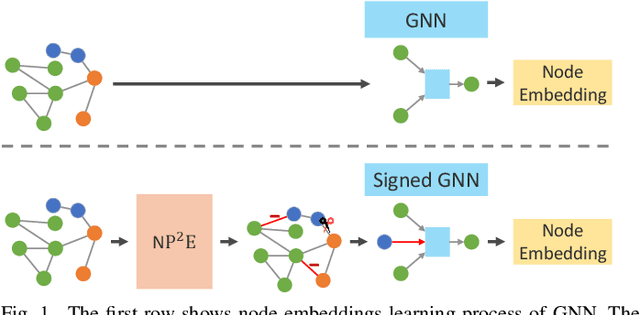
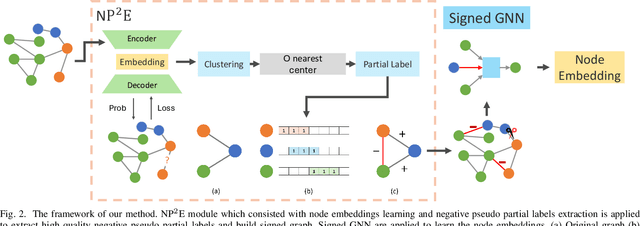
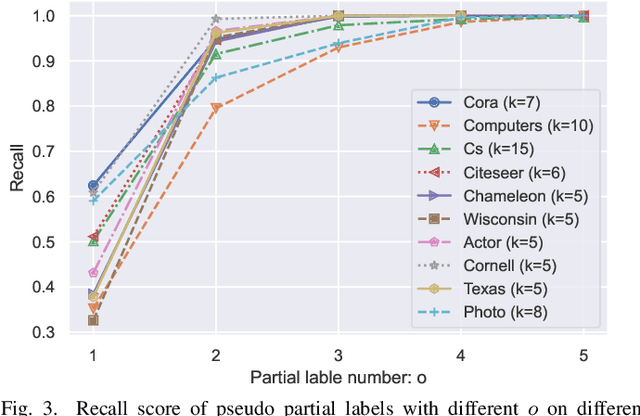
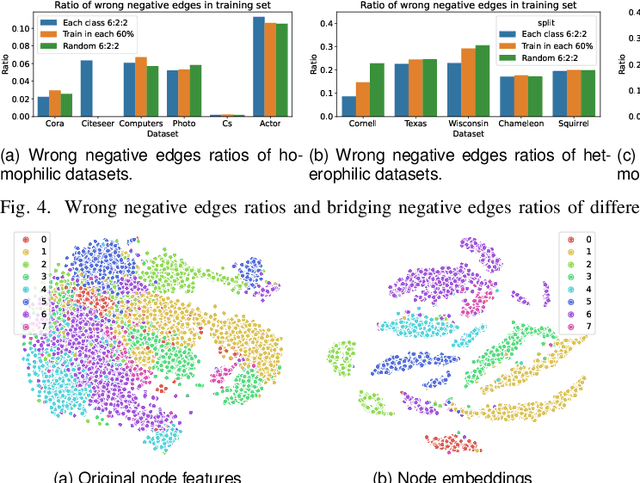
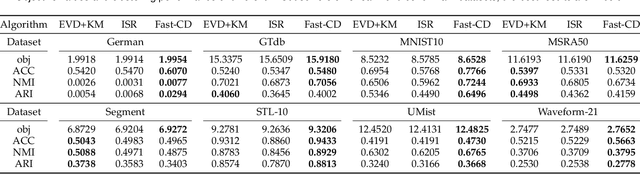
How to utilize the pseudo labels has always been a research hotspot in machine learning. However, most methods use pseudo labels as supervised training, and lack of valid assessing for their accuracy. Moreover, applications of pseudo labels in graph neural networks (GNNs) oversee the difference between graph learning and other machine learning tasks such as message passing mechanism. Aiming to address the first issue, we found through a large number of experiments that the pseudo labels are more accurate if they are selected by not overlapping partial labels and defined as negative node pairs relations. Therefore, considering the extraction based on pseudo and partial labels, negative edges are constructed between two nodes by the negative pseudo partial labels extraction (NP$^2$E) module. With that, a signed graph are built containing highly accurate pseudo labels information from the original graph, which effectively assists GNN in learning at the message-passing level, provide one solution to the second issue. Empirical results about link prediction and node classification tasks on several benchmark datasets demonstrate the effectiveness of our method. State-of-the-art performance is achieved on the both tasks.