A Novel Normalized-Cut Solver with Nearest Neighbor Hierarchical Initialization
Paper and Code
Nov 26, 2023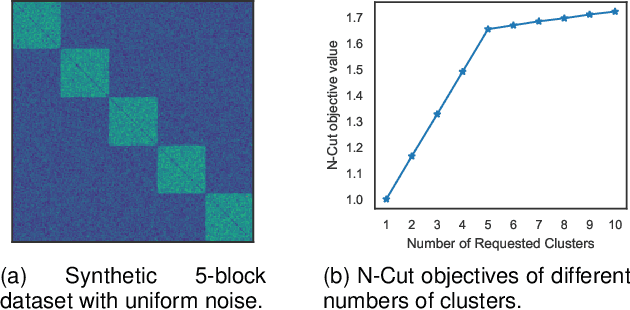
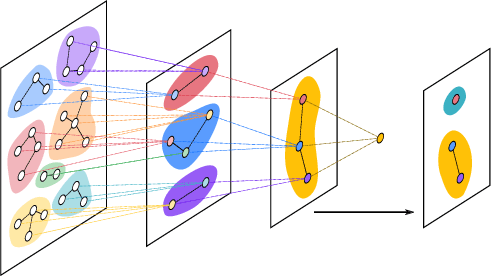
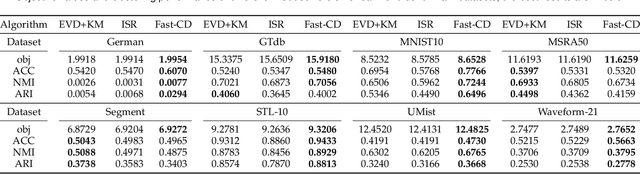
Normalized-Cut (N-Cut) is a famous model of spectral clustering. The traditional N-Cut solvers are two-stage: 1) calculating the continuous spectral embedding of normalized Laplacian matrix; 2) discretization via $K$-means or spectral rotation. However, this paradigm brings two vital problems: 1) two-stage methods solve a relaxed version of the original problem, so they cannot obtain good solutions for the original N-Cut problem; 2) solving the relaxed problem requires eigenvalue decomposition, which has $\mathcal{O}(n^3)$ time complexity ($n$ is the number of nodes). To address the problems, we propose a novel N-Cut solver designed based on the famous coordinate descent method. Since the vanilla coordinate descent method also has $\mathcal{O}(n^3)$ time complexity, we design various accelerating strategies to reduce the time complexity to $\mathcal{O}(|E|)$ ($|E|$ is the number of edges). To avoid reliance on random initialization which brings uncertainties to clustering, we propose an efficient initialization method that gives deterministic outputs. Extensive experiments on several benchmark datasets demonstrate that the proposed solver can obtain larger objective values of N-Cut, meanwhile achieving better clustering performance compared to traditional solvers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge