Flow Shape Design for Microfluidic Devices Using Deep Reinforcement Learning

Microfluidic devices are utilized to control and direct flow behavior in a wide variety of applications, particularly in medical diagnostics. A particularly popular form of microfluidics -- called inertial microfluidic flow sculpting -- involves placing a sequence of pillars to controllably deform an initial flow field into a desired one. Inertial flow sculpting can be formally defined as an inverse problem, where one identifies a sequence of pillars (chosen, with replacement, from a finite set of pillars, each of which produce a specific transformation) whose composite transformation results in a user-defined desired transformation. Endemic to most such problems in engineering, inverse problems are usually quite computationally intractable, with most traditional approaches based on search and optimization strategies. In this paper, we pose this inverse problem as a Reinforcement Learning (RL) problem. We train a DoubleDQN agent to learn from this environment. The results suggest that learning is possible using a DoubleDQN model with the success frequency reaching 90% in 200,000 episodes and the rewards converging. While most of the results are obtained by fixing a particular target flow shape to simplify the learning problem, we later demonstrate how to transfer the learning of an agent based on one target shape to another, i.e. from one design to another and thus be useful for a generic design of a flow shape.

Deep Action Sequence Learning for Causal Shape Transformation

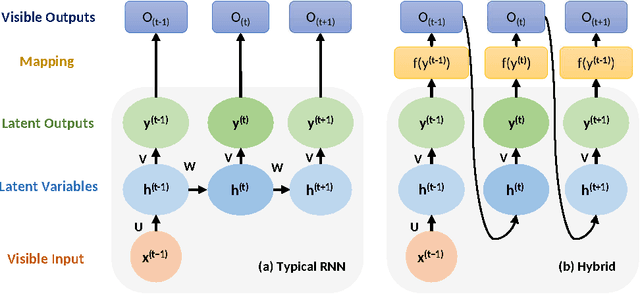
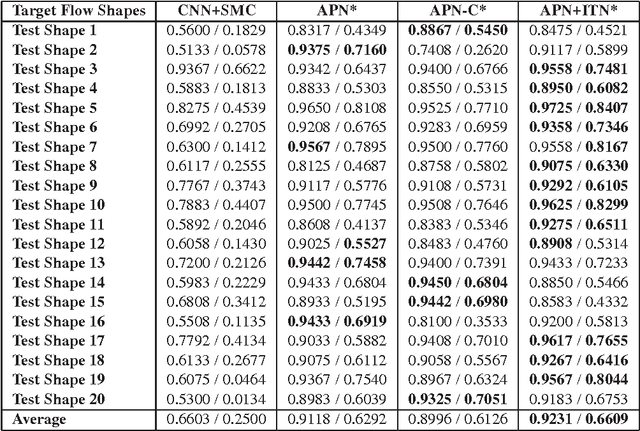
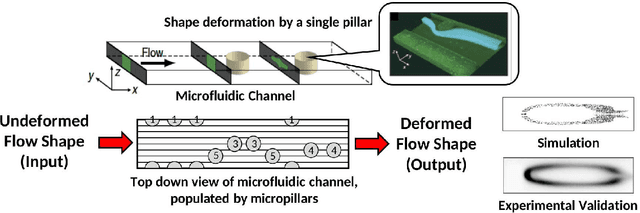
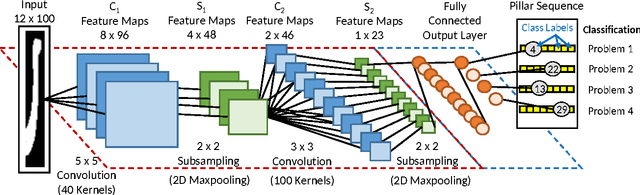
Deep learning became the method of choice in recent year for solving a wide variety of predictive analytics tasks. For sequence prediction, recurrent neural networks (RNN) are often the go-to architecture for exploiting sequential information where the output is dependent on previous computation. However, the dependencies of the computation lie in the latent domain which may not be suitable for certain applications involving the prediction of a step-wise transformation sequence that is dependent on the previous computation only in the visible domain. We propose that a hybrid architecture of convolution neural networks (CNN) and stacked autoencoders (SAE) is sufficient to learn a sequence of actions that nonlinearly transforms an input shape or distribution into a target shape or distribution with the same support. While such a framework can be useful in a variety of problems such as robotic path planning, sequential decision-making in games, and identifying material processing pathways to achieve desired microstructures, the application of the framework is exemplified by the control of fluid deformations in a microfluidic channel by deliberately placing a sequence of pillars. Learning of a multistep topological transform has significant implications for rapid advances in material science and biomedical applications.