Deep Action Sequence Learning for Causal Shape Transformation
Paper and Code
Nov 08, 2016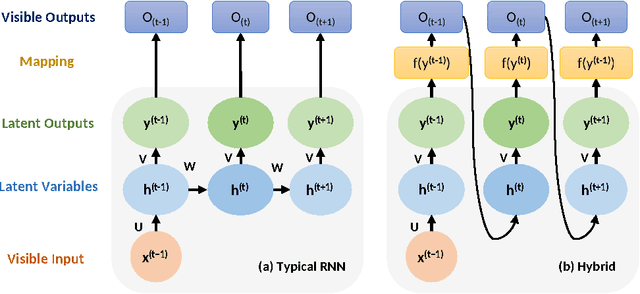
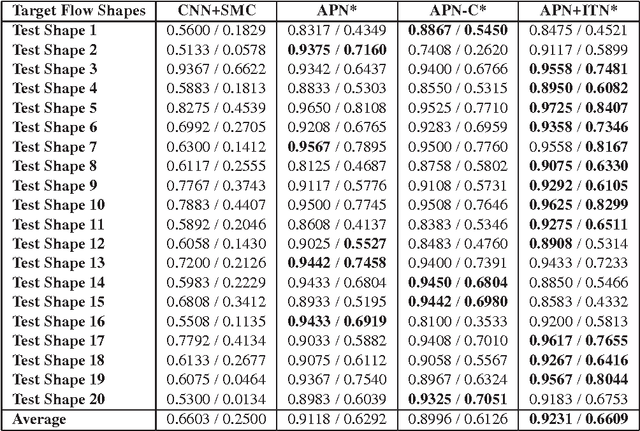
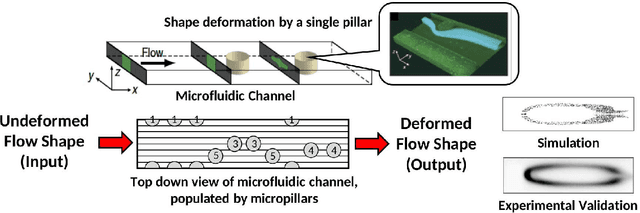
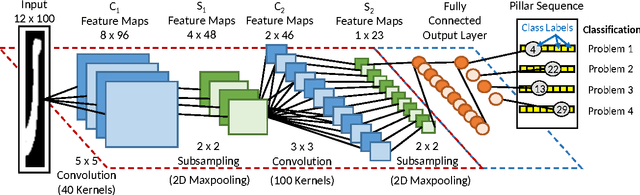
Deep learning became the method of choice in recent year for solving a wide variety of predictive analytics tasks. For sequence prediction, recurrent neural networks (RNN) are often the go-to architecture for exploiting sequential information where the output is dependent on previous computation. However, the dependencies of the computation lie in the latent domain which may not be suitable for certain applications involving the prediction of a step-wise transformation sequence that is dependent on the previous computation only in the visible domain. We propose that a hybrid architecture of convolution neural networks (CNN) and stacked autoencoders (SAE) is sufficient to learn a sequence of actions that nonlinearly transforms an input shape or distribution into a target shape or distribution with the same support. While such a framework can be useful in a variety of problems such as robotic path planning, sequential decision-making in games, and identifying material processing pathways to achieve desired microstructures, the application of the framework is exemplified by the control of fluid deformations in a microfluidic channel by deliberately placing a sequence of pillars. Learning of a multistep topological transform has significant implications for rapid advances in material science and biomedical applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge