An Optimal and Scalable Matrix Mechanism for Noisy Marginals under Convex Loss Functions

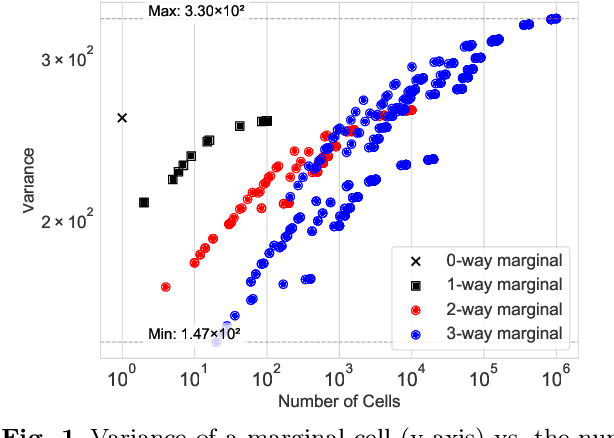
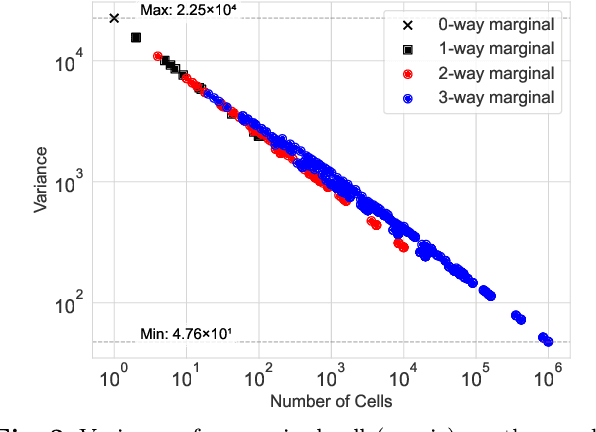
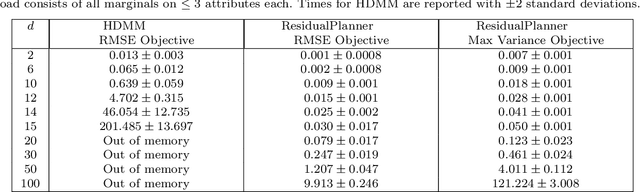
Noisy marginals are a common form of confidentiality-protecting data release and are useful for many downstream tasks such as contingency table analysis, construction of Bayesian networks, and even synthetic data generation. Privacy mechanisms that provide unbiased noisy answers to linear queries (such as marginals) are known as matrix mechanisms. We propose ResidualPlanner, a matrix mechanism for marginals with Gaussian noise that is both optimal and scalable. ResidualPlanner can optimize for many loss functions that can be written as a convex function of marginal variances (prior work was restricted to just one predefined objective function). ResidualPlanner can optimize the accuracy of marginals in large scale settings in seconds, even when the previous state of the art (HDMM) runs out of memory. It even runs on datasets with 100 attributes in a couple of minutes. Furthermore ResidualPlanner can efficiently compute variance/covariance values for each marginal (prior methods quickly run out of memory, even for relatively small datasets).

Answering Private Linear Queries Adaptively using the Common Mechanism

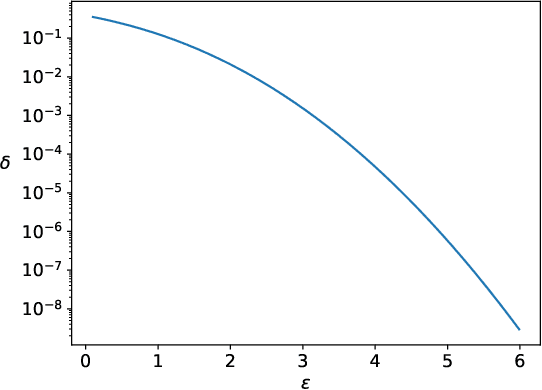
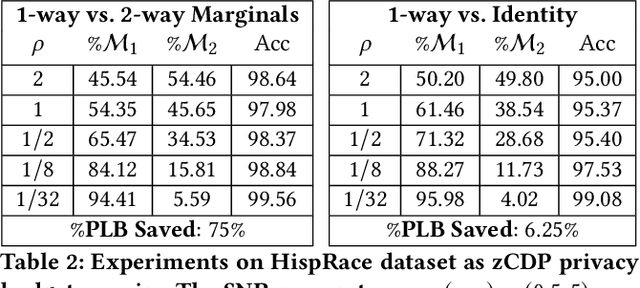
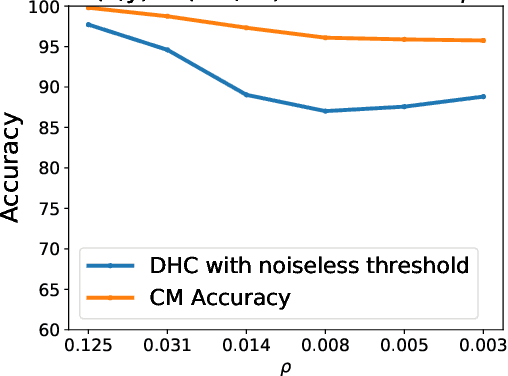
When analyzing confidential data through a privacy filter, a data scientist often needs to decide which queries will best support their intended analysis. For example, an analyst may wish to study noisy two-way marginals in a dataset produced by a mechanism M1. But, if the data are relatively sparse, the analyst may choose to examine noisy one-way marginals, produced by a mechanism M2 instead. Since the choice of whether to use M1 or M2 is data-dependent, a typical differentially private workflow is to first split the privacy loss budget rho into two parts: rho1 and rho2, then use the first part rho1 to determine which mechanism to use, and the remainder rho2 to obtain noisy answers from the chosen mechanism. In a sense, the first step seems wasteful because it takes away part of the privacy loss budget that could have been used to make the query answers more accurate. In this paper, we consider the question of whether the choice between M1 and M2 can be performed without wasting any privacy loss budget. For linear queries, we propose a method for decomposing M1 and M2 into three parts: (1) a mechanism M* that captures their shared information, (2) a mechanism M1' that captures information that is specific to M1, (3) a mechanism M2' that captures information that is specific to M2. Running M* and M1' together is completely equivalent to running M1 (both in terms of query answer accuracy and total privacy cost rho). Similarly, running M* and M2' together is completely equivalent to running M2. Since M* will be used no matter what, the analyst can use its output to decide whether to subsequently run M1'(thus recreating the analysis supported by M1) or M2'(recreating the analysis supported by M2), without wasting privacy loss budget.

Free Gap Information from the Differentially Private Sparse Vector and Noisy Max Mechanisms

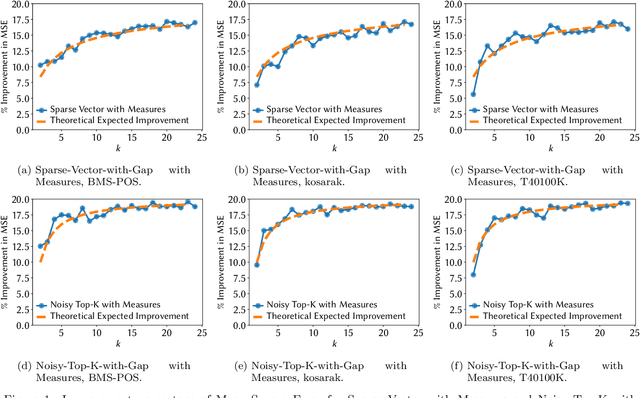
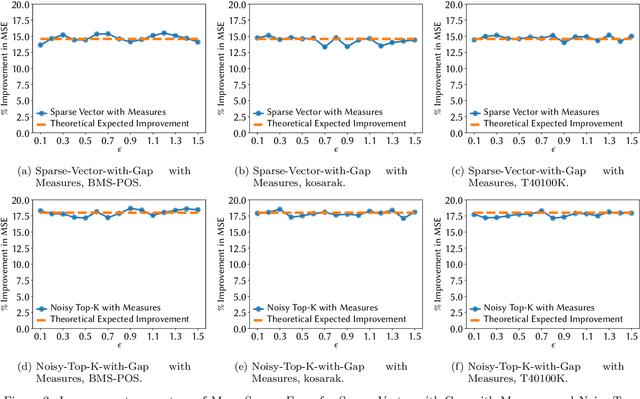
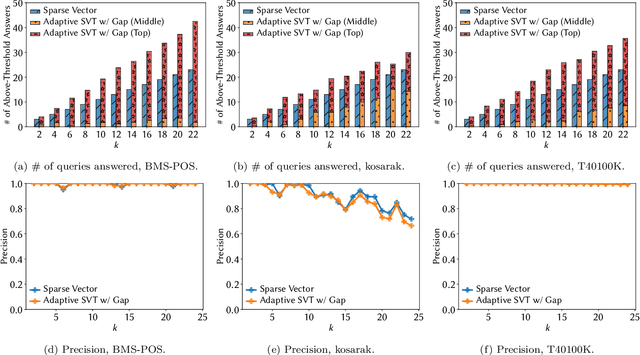
Noisy Max and Sparse Vector are selection algorithms for differential privacy and serve as building blocks for more complex algorithms. In this paper we show that both algorithms can release additional information for free (i.e., at no additional privacy cost). Noisy Max is used to return the approximate maximizer among a set of queries. We show that it can also release for free the noisy gap between the approximate maximizer and runner-up. Sparse Vector is used to return a set of queries that are approximately larger than a fixed threshold. We show that it can adaptively control its privacy budget (use less budget for queries that are likely to be much larger than the threshold) and simultaneously release for free a noisy gap between the selected queries and the threshold. It has long been suspected that Sparse Vector can release additional information, but prior attempts had incorrect proofs. Our version is proved using randomness alignment, a proof template framework borrowed from the program verification literature. We show how the free extra information in both mechanisms can be used to improve the utility of differentially private algorithms.