Free Gap Information from the Differentially Private Sparse Vector and Noisy Max Mechanisms

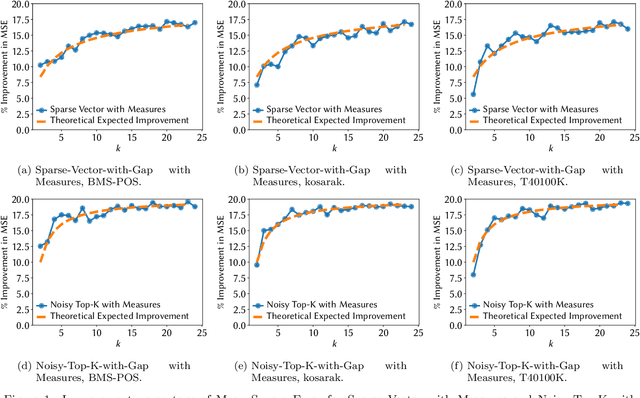
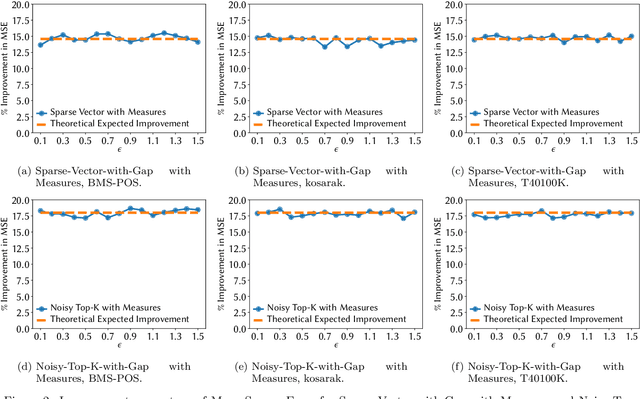
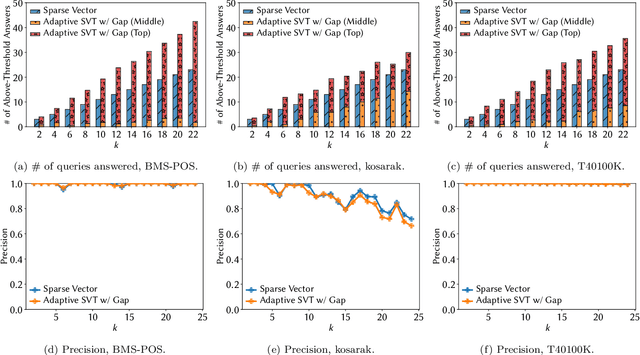
Noisy Max and Sparse Vector are selection algorithms for differential privacy and serve as building blocks for more complex algorithms. In this paper we show that both algorithms can release additional information for free (i.e., at no additional privacy cost). Noisy Max is used to return the approximate maximizer among a set of queries. We show that it can also release for free the noisy gap between the approximate maximizer and runner-up. Sparse Vector is used to return a set of queries that are approximately larger than a fixed threshold. We show that it can adaptively control its privacy budget (use less budget for queries that are likely to be much larger than the threshold) and simultaneously release for free a noisy gap between the selected queries and the threshold. It has long been suspected that Sparse Vector can release additional information, but prior attempts had incorrect proofs. Our version is proved using randomness alignment, a proof template framework borrowed from the program verification literature. We show how the free extra information in both mechanisms can be used to improve the utility of differentially private algorithms.