Toward Trustworthy AI: Multi-Target Adversarial Attacks and Robust Defenses for Continuous Data Summarization

Trustworthy AI requires reliable data-processing pipelines, not only robust downstream predictive models. As an upstream component, data summarization determines which information is retained and passed to subsequent learning or decision modules. Therefore, adversarial perturbations to the summarization process can compromise trustworthy AI in an upstream manner: they may alter the selected summary, reduce its representativeness, and further degrade the utility of subsequent learning tasks. In this paper, we study adversarial attacks on continuous data summarization under similarity-level perturbations through DR-submodular optimization. We show that a class of multi-resolution image summarization objectives can be formulated as multilinear extensions of non-negative submodular set functions and satisfy DR-submodularity with $m$-weak monotonicity. We then formulate multi-target attack generation as a min-max problem, where one admissible perturbation of the similarity structure is optimized to degrade multiple target summarization models. To mitigate such perturbations, we formulate robust defense against mixed attack types as a regularized max-min problem. For both problems, we develop approximation algorithms with theoretical guarantees. Experiments on real-data and controlled clustered benchmarks show that the proposed attack is effective in representative low-to-moderate budget regimes and can induce downstream task-performance loss. The proposed defense improves the robustness--mitigation trade-off in structured settings, while also revealing the parameter sensitivity of robust protection on real data.

A Provably Convergent Plug-and-Play Framework for Stochastic Bilevel Optimization

Bilevel optimization has recently attracted significant attention in machine learning due to its wide range of applications and advanced hierarchical optimization capabilities. In this paper, we propose a plug-and-play framework, named PnPBO, for developing and analyzing stochastic bilevel optimization methods. This framework integrates both modern unbiased and biased stochastic estimators into the single-loop bilevel optimization framework introduced in [9], with several improvements. In the implementation of PnPBO, all stochastic estimators for different variables can be independently incorporated, and an additional moving average technique is applied when using an unbiased estimator for the upper-level variable. In the theoretical analysis, we provide a unified convergence and complexity analysis for PnPBO, demonstrating that the adaptation of various stochastic estimators (including PAGE, ZeroSARAH, and mixed strategies) within the PnPBO framework achieves optimal sample complexity, comparable to that of single-level optimization. This resolves the open question of whether the optimal complexity bounds for solving bilevel optimization are identical to those for single-level optimization. Finally, we empirically validate our framework, demonstrating its effectiveness on several benchmark problems and confirming our theoretical findings.

SPABA: A Single-Loop and Probabilistic Stochastic Bilevel Algorithm Achieving Optimal Sample Complexity

While stochastic bilevel optimization methods have been extensively studied for addressing large-scale nested optimization problems in machine learning, it remains an open question whether the optimal complexity bounds for solving bilevel optimization are the same as those in single-level optimization. Our main result resolves this question: SPABA, an adaptation of the PAGE method for nonconvex optimization in (Li et al., 2021) to the bilevel setting, can achieve optimal sample complexity in both the finite-sum and expectation settings. We show the optimality of SPABA by proving that there is no gap in complexity analysis between stochastic bilevel and single-level optimization when implementing PAGE. Notably, as indicated by the results of (Dagr\'eou et al., 2022), there might exist a gap in complexity analysis when implementing other stochastic gradient estimators, like SGD and SAGA. In addition to SPABA, we propose several other single-loop stochastic bilevel algorithms, that either match or improve the state-of-the-art sample complexity results, leveraging our convergence rate and complexity analysis. Numerical experiments demonstrate the superior practical performance of the proposed methods.

Eigenvalue-corrected Natural Gradient Based on a New Approximation

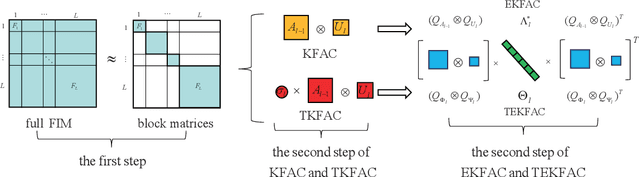
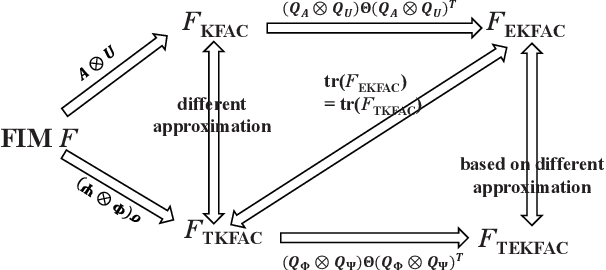
Using second-order optimization methods for training deep neural networks (DNNs) has attracted many researchers. A recently proposed method, Eigenvalue-corrected Kronecker Factorization (EKFAC) (George et al., 2018), proposes an interpretation of viewing natural gradient update as a diagonal method, and corrects the inaccurate re-scaling factor in the Kronecker-factored eigenbasis. Gao et al. (2020) considers a new approximation to the natural gradient, which approximates the Fisher information matrix (FIM) to a constant multiplied by the Kronecker product of two matrices and keeps the trace equal before and after the approximation. In this work, we combine the ideas of these two methods and propose Trace-restricted Eigenvalue-corrected Kronecker Factorization (TEKFAC). The proposed method not only corrects the inexact re-scaling factor under the Kronecker-factored eigenbasis, but also considers the new approximation method and the effective damping technique proposed in Gao et al. (2020). We also discuss the differences and relationships among the Kronecker-factored approximations. Empirically, our method outperforms SGD with momentum, Adam, EKFAC and TKFAC on several DNNs.

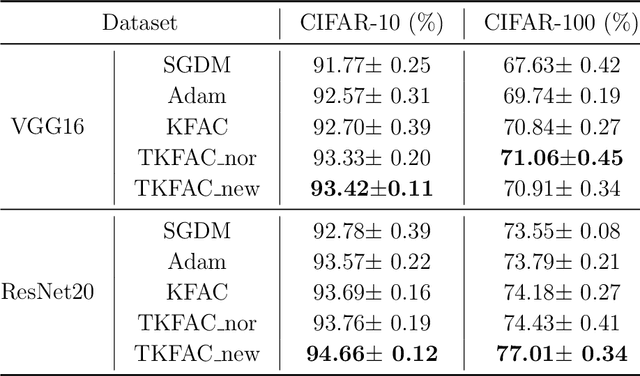
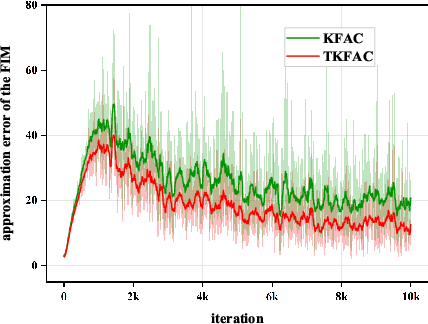
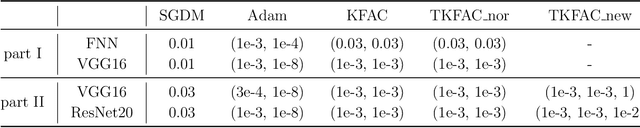
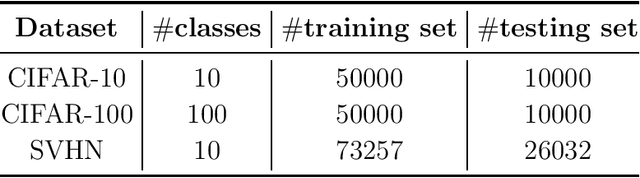
A Trace-restricted Kronecker-Factored Approximation to Natural Gradient

Second-order optimization methods have the ability to accelerate convergence by modifying the gradient through the curvature matrix. There have been many attempts to use second-order optimization methods for training deep neural networks. Inspired by diagonal approximations and factored approximations such as Kronecker-Factored Approximate Curvature (KFAC), we propose a new approximation to the Fisher information matrix (FIM) called Trace-restricted Kronecker-factored Approximate Curvature (TKFAC) in this work, which can hold the certain trace relationship between the exact and the approximate FIM. In TKFAC, we decompose each block of the approximate FIM as a Kronecker product of two smaller matrices and scaled by a coefficient related to trace. We theoretically analyze TKFAC's approximation error and give an upper bound of it. We also propose a new damping technique for TKFAC on convolutional neural networks to maintain the superiority of second-order optimization methods during training. Experiments show that our method has better performance compared with several state-of-the-art algorithms on some deep network architectures.