Eigenvalue-corrected Natural Gradient Based on a New Approximation

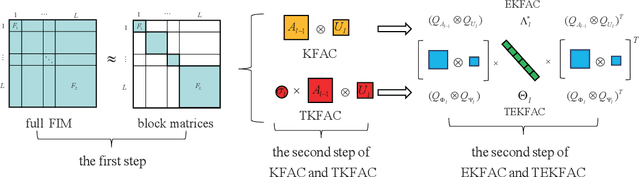
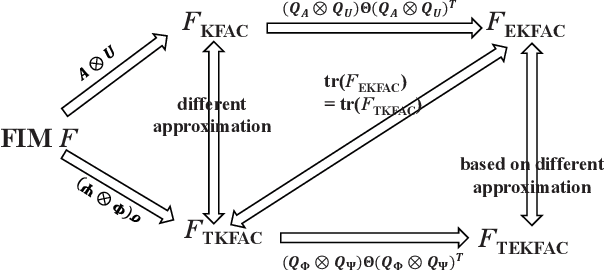
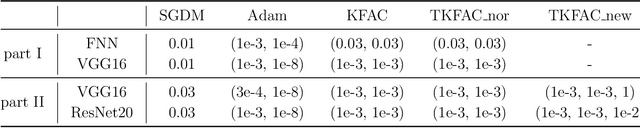
Using second-order optimization methods for training deep neural networks (DNNs) has attracted many researchers. A recently proposed method, Eigenvalue-corrected Kronecker Factorization (EKFAC) (George et al., 2018), proposes an interpretation of viewing natural gradient update as a diagonal method, and corrects the inaccurate re-scaling factor in the Kronecker-factored eigenbasis. Gao et al. (2020) considers a new approximation to the natural gradient, which approximates the Fisher information matrix (FIM) to a constant multiplied by the Kronecker product of two matrices and keeps the trace equal before and after the approximation. In this work, we combine the ideas of these two methods and propose Trace-restricted Eigenvalue-corrected Kronecker Factorization (TEKFAC). The proposed method not only corrects the inexact re-scaling factor under the Kronecker-factored eigenbasis, but also considers the new approximation method and the effective damping technique proposed in Gao et al. (2020). We also discuss the differences and relationships among the Kronecker-factored approximations. Empirically, our method outperforms SGD with momentum, Adam, EKFAC and TKFAC on several DNNs.

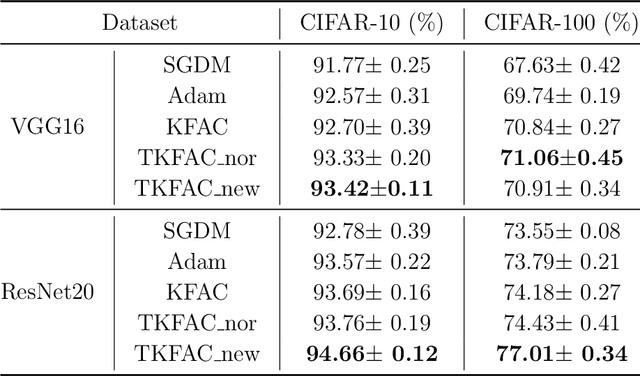
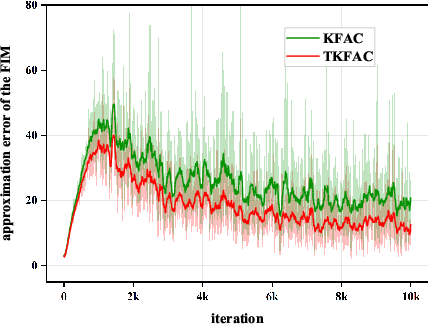
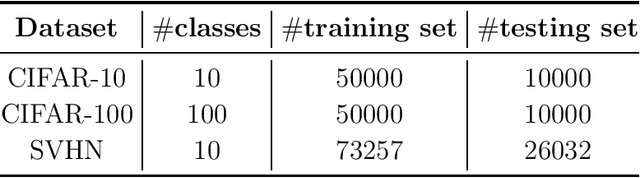
A Trace-restricted Kronecker-Factored Approximation to Natural Gradient

Second-order optimization methods have the ability to accelerate convergence by modifying the gradient through the curvature matrix. There have been many attempts to use second-order optimization methods for training deep neural networks. Inspired by diagonal approximations and factored approximations such as Kronecker-Factored Approximate Curvature (KFAC), we propose a new approximation to the Fisher information matrix (FIM) called Trace-restricted Kronecker-factored Approximate Curvature (TKFAC) in this work, which can hold the certain trace relationship between the exact and the approximate FIM. In TKFAC, we decompose each block of the approximate FIM as a Kronecker product of two smaller matrices and scaled by a coefficient related to trace. We theoretically analyze TKFAC's approximation error and give an upper bound of it. We also propose a new damping technique for TKFAC on convolutional neural networks to maintain the superiority of second-order optimization methods during training. Experiments show that our method has better performance compared with several state-of-the-art algorithms on some deep network architectures.

Minimum $n$-Rank Approximation via Iterative Hard Thresholding

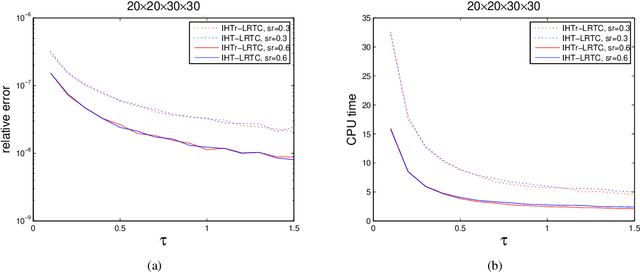
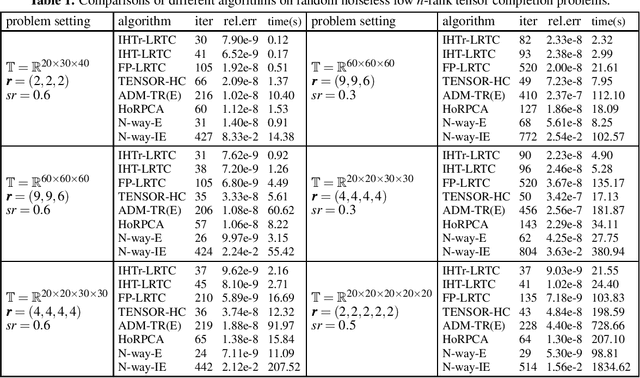
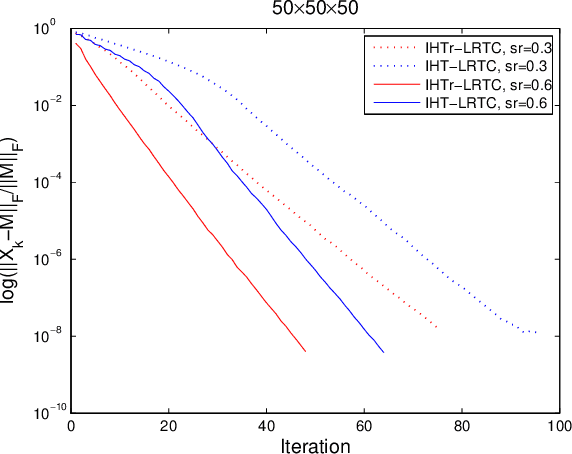
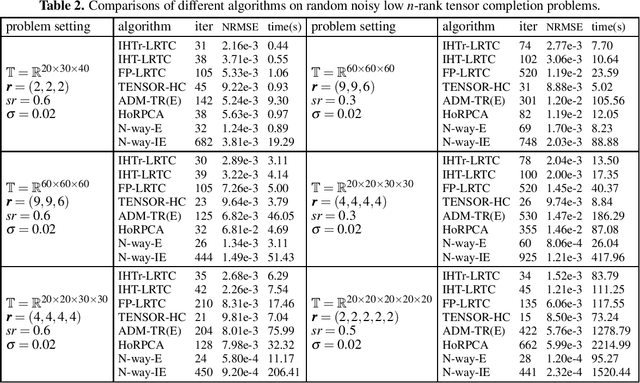
The problem of recovering a low $n$-rank tensor is an extension of sparse recovery problem from the low dimensional space (matrix space) to the high dimensional space (tensor space) and has many applications in computer vision and graphics such as image inpainting and video inpainting. In this paper, we consider a new tensor recovery model, named as minimum $n$-rank approximation (MnRA), and propose an appropriate iterative hard thresholding algorithm with giving the upper bound of the $n$-rank in advance. The convergence analysis of the proposed algorithm is also presented. Particularly, we show that for the noiseless case, the linear convergence with rate $\frac{1}{2}$ can be obtained for the proposed algorithm under proper conditions. Additionally, combining an effective heuristic for determining $n$-rank, we can also apply the proposed algorithm to solve MnRA when $n$-rank is unknown in advance. Some preliminary numerical results on randomly generated and real low $n$-rank tensor completion problems are reported, which show the efficiency of the proposed algorithms.