Cosimo Rulli
Effective Inference-Free Retrieval for Learned Sparse Representations
Apr 30, 2025Abstract:Learned Sparse Retrieval (LSR) is an effective IR approach that exploits pre-trained language models for encoding text into a learned bag of words. Several efforts in the literature have shown that sparsity is key to enabling a good trade-off between the efficiency and effectiveness of the query processor. To induce the right degree of sparsity, researchers typically use regularization techniques when training LSR models. Recently, new efficient -- inverted index-based -- retrieval engines have been proposed, leading to a natural question: has the role of regularization changed in training LSR models? In this paper, we conduct an extended evaluation of regularization approaches for LSR where we discuss their effectiveness, efficiency, and out-of-domain generalization capabilities. We first show that regularization can be relaxed to produce more effective LSR encoders. We also show that query encoding is now the bottleneck limiting the overall query processor performance. To remove this bottleneck, we advance the state-of-the-art of inference-free LSR by proposing Learned Inference-free Retrieval (Li-LSR). At training time, Li-LSR learns a score for each token, casting the query encoding step into a seamless table lookup. Our approach yields state-of-the-art effectiveness for both in-domain and out-of-domain evaluation, surpassing Splade-v3-Doc by 1 point of mRR@10 on MS MARCO and 1.8 points of nDCG@10 on BEIR.
Efficient Conversational Search via Topical Locality in Dense Retrieval
Apr 30, 2025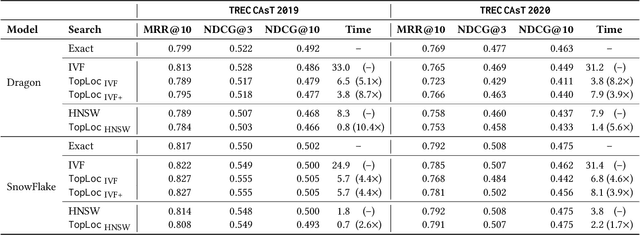
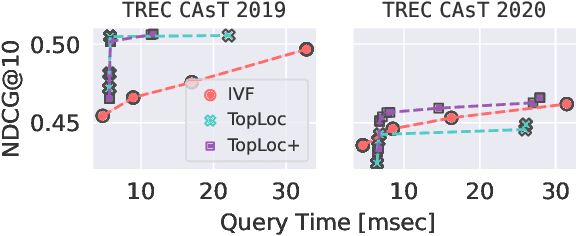
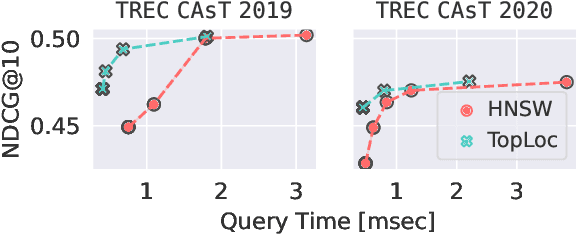
Abstract:Pre-trained language models have been widely exploited to learn dense representations of documents and queries for information retrieval. While previous efforts have primarily focused on improving effectiveness and user satisfaction, response time remains a critical bottleneck of conversational search systems. To address this, we exploit the topical locality inherent in conversational queries, i.e., the tendency of queries within a conversation to focus on related topics. By leveraging query embedding similarities, we dynamically restrict the search space to semantically relevant document clusters, reducing computational complexity without compromising retrieval quality. We evaluate our approach on the TREC CAsT 2019 and 2020 datasets using multiple embedding models and vector indexes, achieving improvements in processing speed of up to 10.4X with little loss in performance (4.4X without any loss). Our results show that the proposed system effectively handles complex, multiturn queries with high precision and efficiency, offering a practical solution for real-time conversational search.
Investigating the Scalability of Approximate Sparse Retrieval Algorithms to Massive Datasets
Jan 20, 2025


Abstract:Learned sparse text embeddings have gained popularity due to their effectiveness in top-k retrieval and inherent interpretability. Their distributional idiosyncrasies, however, have long hindered their use in real-world retrieval systems. That changed with the recent development of approximate algorithms that leverage the distributional properties of sparse embeddings to speed up retrieval. Nonetheless, in much of the existing literature, evaluation has been limited to datasets with only a few million documents such as MSMARCO. It remains unclear how these systems behave on much larger datasets and what challenges lurk in larger scales. To bridge that gap, we investigate the behavior of state-of-the-art retrieval algorithms on massive datasets. We compare and contrast the recently-proposed Seismic and graph-based solutions adapted from dense retrieval. We extensively evaluate Splade embeddings of 138M passages from MsMarco-v2 and report indexing time and other efficiency and effectiveness metrics.
kANNolo: Sweet and Smooth Approximate k-Nearest Neighbors Search
Jan 10, 2025Abstract:Approximate Nearest Neighbors (ANN) search is a crucial task in several applications like recommender systems and information retrieval. Current state-of-the-art ANN libraries, although being performance-oriented, often lack modularity and ease of use. This translates into them not being fully suitable for easy prototyping and testing of research ideas, an important feature to enable. We address these limitations by introducing kANNolo, a novel research-oriented ANN library written in Rust and explicitly designed to combine usability with performance effectively. kANNolo is the first ANN library that supports dense and sparse vector representations made available on top of different similarity measures, e.g., euclidean distance and inner product. Moreover, it also supports vector quantization techniques, e.g., Product Quantization, on top of the indexing strategies implemented. These functionalities are managed through Rust traits, allowing shared behaviors to be handled abstractly. This abstraction ensures flexibility and facilitates an easy integration of new components. In this work, we detail the architecture of kANNolo and demonstrate that its flexibility does not compromise performance. The experimental analysis shows that kANNolo achieves state-of-the-art performance in terms of speed-accuracy trade-off while allowing fast and easy prototyping, thus making kANNolo a valuable tool for advancing ANN research. Source code available on GitHub: https://github.com/TusKANNy/kannolo.
Pairing Clustered Inverted Indexes with kNN Graphs for Fast Approximate Retrieval over Learned Sparse Representations
Aug 08, 2024



Abstract:Learned sparse representations form an effective and interpretable class of embeddings for text retrieval. While exact top-k retrieval over such embeddings faces efficiency challenges, a recent algorithm called Seismic has enabled remarkably fast, highly-accurate approximate retrieval. Seismic statically prunes inverted lists, organizes each list into geometrically-cohesive blocks, and augments each block with a summary vector. At query time, each inverted list associated with a query term is traversed one block at a time in an arbitrary order, with the inner product between the query and summaries determining if a block must be evaluated. When a block is deemed promising, its documents are fully evaluated with a forward index. Seismic is one to two orders of magnitude faster than state-of-the-art inverted index-based solutions and significantly outperforms the winning graph-based submissions to the BigANN 2023 Challenge. In this work, we speed up Seismic further by introducing two innovations to its query processing subroutine. First, we traverse blocks in order of importance, rather than arbitrarily. Second, we take the list of documents retrieved by Seismic and expand it to include the neighbors of each document using an offline k-regular nearest neighbor graph; the expanded list is then ranked to produce the final top-k set. Experiments on two public datasets show that our extension, named SeismicWave, can reach almost-exact accuracy levels and is up to 2.2x faster than Seismic.
Efficient Inverted Indexes for Approximate Retrieval over Learned Sparse Representations
Apr 29, 2024



Abstract:Learned sparse representations form an attractive class of contextual embeddings for text retrieval. That is so because they are effective models of relevance and are interpretable by design. Despite their apparent compatibility with inverted indexes, however, retrieval over sparse embeddings remains challenging. That is due to the distributional differences between learned embeddings and term frequency-based lexical models of relevance such as BM25. Recognizing this challenge, a great deal of research has gone into, among other things, designing retrieval algorithms tailored to the properties of learned sparse representations, including approximate retrieval systems. In fact, this task featured prominently in the latest BigANN Challenge at NeurIPS 2023, where approximate algorithms were evaluated on a large benchmark dataset by throughput and recall. In this work, we propose a novel organization of the inverted index that enables fast yet effective approximate retrieval over learned sparse embeddings. Our approach organizes inverted lists into geometrically-cohesive blocks, each equipped with a summary vector. During query processing, we quickly determine if a block must be evaluated using the summaries. As we show experimentally, single-threaded query processing using our method, Seismic, reaches sub-millisecond per-query latency on various sparse embeddings of the MS MARCO dataset while maintaining high recall. Our results indicate that Seismic is one to two orders of magnitude faster than state-of-the-art inverted index-based solutions and further outperforms the winning (graph-based) submissions to the BigANN Challenge by a significant margin.
Efficient Multi-Vector Dense Retrieval Using Bit Vectors
Apr 03, 2024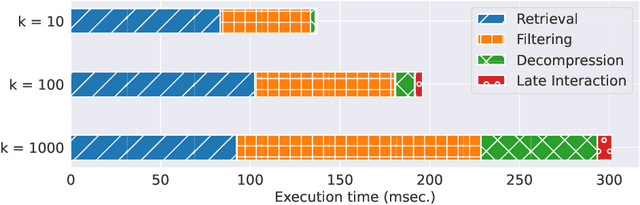
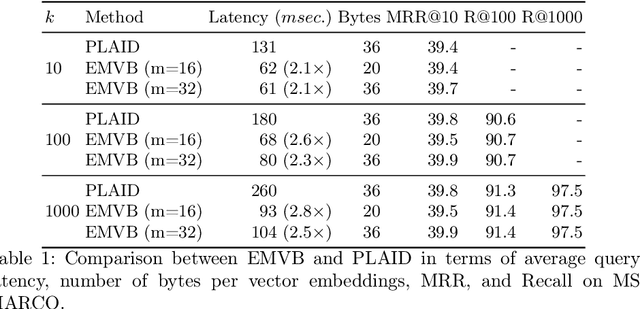
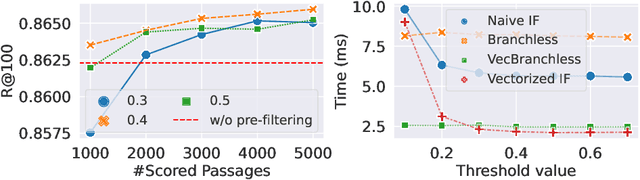

Abstract:Dense retrieval techniques employ pre-trained large language models to build a high-dimensional representation of queries and passages. These representations compute the relevance of a passage w.r.t. to a query using efficient similarity measures. In this line, multi-vector representations show improved effectiveness at the expense of a one-order-of-magnitude increase in memory footprint and query latency by encoding queries and documents on a per-token level. Recently, PLAID has tackled these problems by introducing a centroid-based term representation to reduce the memory impact of multi-vector systems. By exploiting a centroid interaction mechanism, PLAID filters out non-relevant documents, thus reducing the cost of the successive ranking stages. This paper proposes ``Efficient Multi-Vector dense retrieval with Bit vectors'' (EMVB), a novel framework for efficient query processing in multi-vector dense retrieval. First, EMVB employs a highly efficient pre-filtering step of passages using optimized bit vectors. Second, the computation of the centroid interaction happens column-wise, exploiting SIMD instructions, thus reducing its latency. Third, EMVB leverages Product Quantization (PQ) to reduce the memory footprint of storing vector representations while jointly allowing for fast late interaction. Fourth, we introduce a per-document term filtering method that further improves the efficiency of the last step. Experiments on MS MARCO and LoTTE show that EMVB is up to 2.8x faster while reducing the memory footprint by 1.8x with no loss in retrieval accuracy compared to PLAID.
Neural Network Compression using Binarization and Few Full-Precision Weights
Jun 15, 2023Abstract:Quantization and pruning are known to be two effective Deep Neural Networks model compression methods. In this paper, we propose Automatic Prune Binarization (APB), a novel compression technique combining quantization with pruning. APB enhances the representational capability of binary networks using a few full-precision weights. Our technique jointly maximizes the accuracy of the network while minimizing its memory impact by deciding whether each weight should be binarized or kept in full precision. We show how to efficiently perform a forward pass through layers compressed using APB by decomposing it into a binary and a sparse-dense matrix multiplication. Moreover, we design two novel efficient algorithms for extremely quantized matrix multiplication on CPU, leveraging highly efficient bitwise operations. The proposed algorithms are 6.9x and 1.5x faster than available state-of-the-art solutions. We perform an extensive evaluation of APB on two widely adopted model compression datasets, namely CIFAR10 and ImageNet. APB shows to deliver better accuracy/memory trade-off compared to state-of-the-art methods based on i) quantization, ii) pruning, and iii) combination of pruning and quantization. APB outperforms quantization also in the accuracy/efficiency trade-off, being up to 2x faster than the 2-bits quantized model with no loss in accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge