Pairing Clustered Inverted Indexes with kNN Graphs for Fast Approximate Retrieval over Learned Sparse Representations

Learned sparse representations form an effective and interpretable class of embeddings for text retrieval. While exact top-k retrieval over such embeddings faces efficiency challenges, a recent algorithm called Seismic has enabled remarkably fast, highly-accurate approximate retrieval. Seismic statically prunes inverted lists, organizes each list into geometrically-cohesive blocks, and augments each block with a summary vector. At query time, each inverted list associated with a query term is traversed one block at a time in an arbitrary order, with the inner product between the query and summaries determining if a block must be evaluated. When a block is deemed promising, its documents are fully evaluated with a forward index. Seismic is one to two orders of magnitude faster than state-of-the-art inverted index-based solutions and significantly outperforms the winning graph-based submissions to the BigANN 2023 Challenge. In this work, we speed up Seismic further by introducing two innovations to its query processing subroutine. First, we traverse blocks in order of importance, rather than arbitrarily. Second, we take the list of documents retrieved by Seismic and expand it to include the neighbors of each document using an offline k-regular nearest neighbor graph; the expanded list is then ranked to produce the final top-k set. Experiments on two public datasets show that our extension, named SeismicWave, can reach almost-exact accuracy levels and is up to 2.2x faster than Seismic.

Efficient Inverted Indexes for Approximate Retrieval over Learned Sparse Representations

Learned sparse representations form an attractive class of contextual embeddings for text retrieval. That is so because they are effective models of relevance and are interpretable by design. Despite their apparent compatibility with inverted indexes, however, retrieval over sparse embeddings remains challenging. That is due to the distributional differences between learned embeddings and term frequency-based lexical models of relevance such as BM25. Recognizing this challenge, a great deal of research has gone into, among other things, designing retrieval algorithms tailored to the properties of learned sparse representations, including approximate retrieval systems. In fact, this task featured prominently in the latest BigANN Challenge at NeurIPS 2023, where approximate algorithms were evaluated on a large benchmark dataset by throughput and recall. In this work, we propose a novel organization of the inverted index that enables fast yet effective approximate retrieval over learned sparse embeddings. Our approach organizes inverted lists into geometrically-cohesive blocks, each equipped with a summary vector. During query processing, we quickly determine if a block must be evaluated using the summaries. As we show experimentally, single-threaded query processing using our method, Seismic, reaches sub-millisecond per-query latency on various sparse embeddings of the MS MARCO dataset while maintaining high recall. Our results indicate that Seismic is one to two orders of magnitude faster than state-of-the-art inverted index-based solutions and further outperforms the winning (graph-based) submissions to the BigANN Challenge by a significant margin.

Efficient Multi-Vector Dense Retrieval Using Bit Vectors

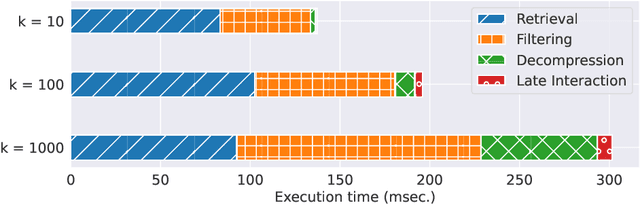
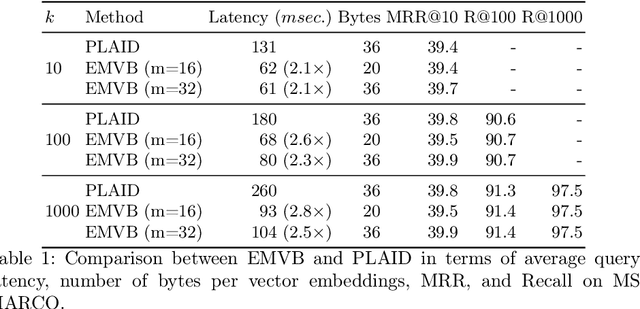
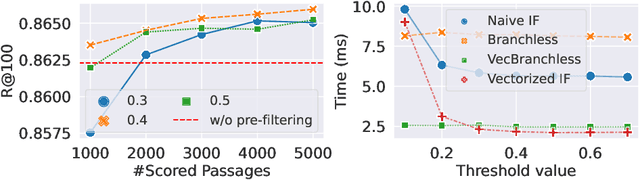
Dense retrieval techniques employ pre-trained large language models to build a high-dimensional representation of queries and passages. These representations compute the relevance of a passage w.r.t. to a query using efficient similarity measures. In this line, multi-vector representations show improved effectiveness at the expense of a one-order-of-magnitude increase in memory footprint and query latency by encoding queries and documents on a per-token level. Recently, PLAID has tackled these problems by introducing a centroid-based term representation to reduce the memory impact of multi-vector systems. By exploiting a centroid interaction mechanism, PLAID filters out non-relevant documents, thus reducing the cost of the successive ranking stages. This paper proposes ``Efficient Multi-Vector dense retrieval with Bit vectors'' (EMVB), a novel framework for efficient query processing in multi-vector dense retrieval. First, EMVB employs a highly efficient pre-filtering step of passages using optimized bit vectors. Second, the computation of the centroid interaction happens column-wise, exploiting SIMD instructions, thus reducing its latency. Third, EMVB leverages Product Quantization (PQ) to reduce the memory footprint of storing vector representations while jointly allowing for fast late interaction. Fourth, we introduce a per-document term filtering method that further improves the efficiency of the last step. Experiments on MS MARCO and LoTTE show that EMVB is up to 2.8x faster while reducing the memory footprint by 1.8x with no loss in retrieval accuracy compared to PLAID.

Neural Network Compression using Binarization and Few Full-Precision Weights

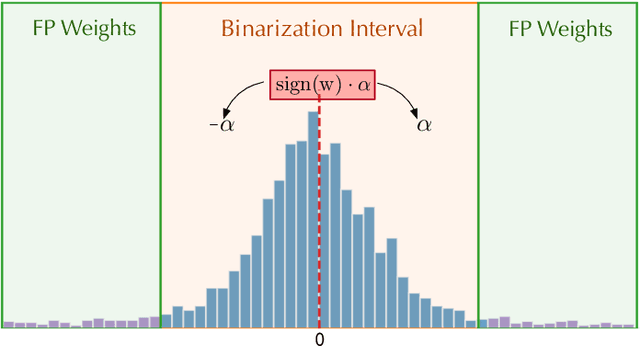
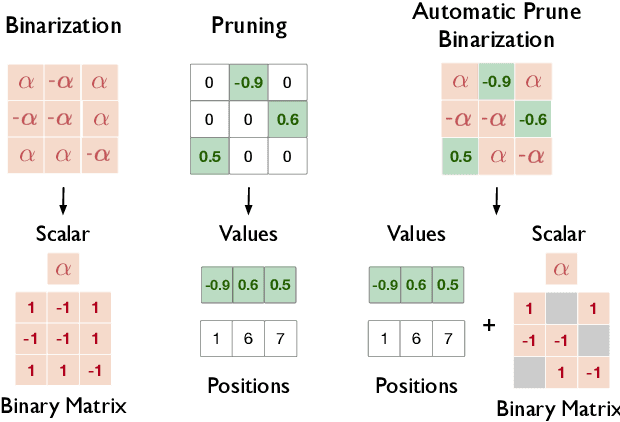
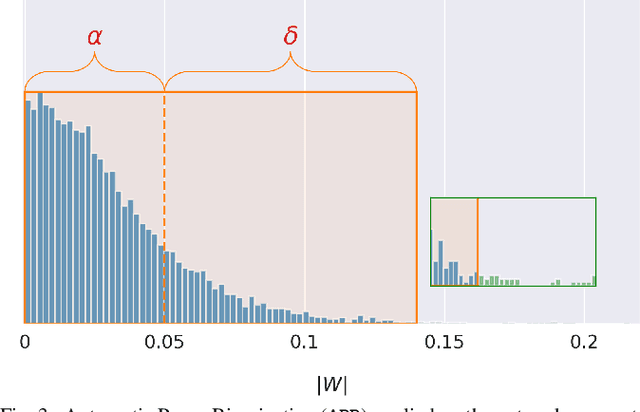
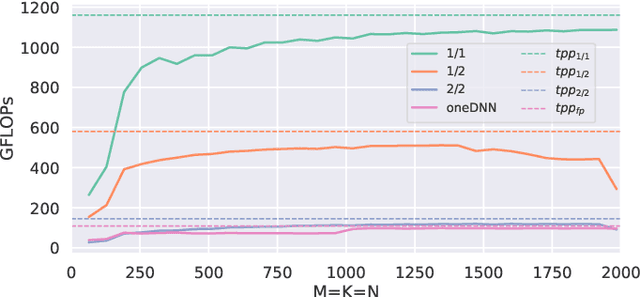
Quantization and pruning are known to be two effective Deep Neural Networks model compression methods. In this paper, we propose Automatic Prune Binarization (APB), a novel compression technique combining quantization with pruning. APB enhances the representational capability of binary networks using a few full-precision weights. Our technique jointly maximizes the accuracy of the network while minimizing its memory impact by deciding whether each weight should be binarized or kept in full precision. We show how to efficiently perform a forward pass through layers compressed using APB by decomposing it into a binary and a sparse-dense matrix multiplication. Moreover, we design two novel efficient algorithms for extremely quantized matrix multiplication on CPU, leveraging highly efficient bitwise operations. The proposed algorithms are 6.9x and 1.5x faster than available state-of-the-art solutions. We perform an extensive evaluation of APB on two widely adopted model compression datasets, namely CIFAR10 and ImageNet. APB shows to deliver better accuracy/memory trade-off compared to state-of-the-art methods based on i) quantization, ii) pruning, and iii) combination of pruning and quantization. APB outperforms quantization also in the accuracy/efficiency trade-off, being up to 2x faster than the 2-bits quantized model with no loss in accuracy.

An Optimal Algorithm for Finding Champions in Tournament Graphs

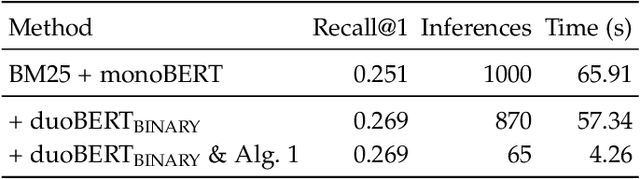
A tournament graph $T = \left(V, E \right)$ is an oriented complete graph, which can be used to model a round-robin tournament between $n$ players. In this paper, we address the problem of finding a champion of the tournament, also known as Copeland winner, which is a player that wins the highest number of matches. Solving this problem has important implications on several Information Retrieval applications, including Web search, conversational IR, machine translation, question answering, recommender systems, etc. Our goal is to solve the problem by minimizing the number of times we probe the adjacency matrix, i.e., the number of matches played. We prove that any deterministic/randomized algorithm finding a champion with constant success probability requires $\Omega(\ell n)$ comparisons, where $\ell$ is the number of matches lost by the champion. We then present an optimal deterministic algorithm matching this lower bound without knowing $\ell$ and we extend our analysis to three strictly related problems. Lastly, we conduct a comprehensive experimental assessment of the proposed algorithms to speed up a state-of-the-art solution for ranking on public data. Results show that our proposals speed up the retrieval of the champion up to $13\times$ in this scenario.