Multiple importance sampling for stochastic gradient estimation

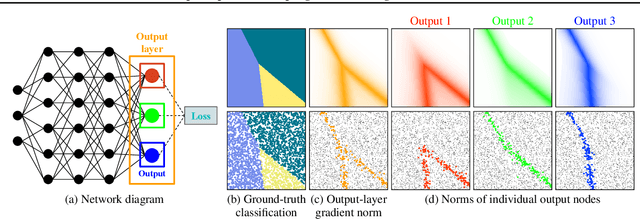
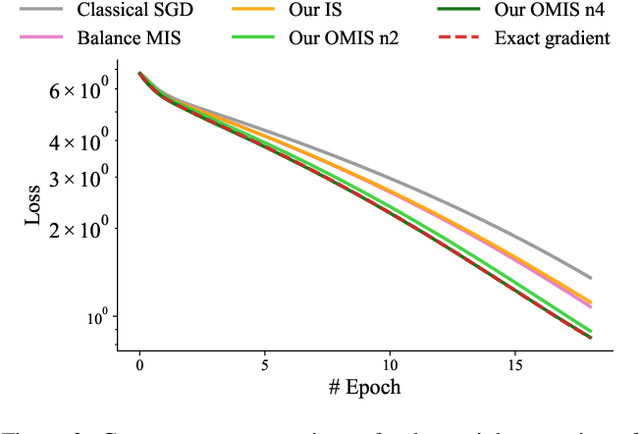
We introduce a theoretical and practical framework for efficient importance sampling of mini-batch samples for gradient estimation from single and multiple probability distributions. To handle noisy gradients, our framework dynamically evolves the importance distribution during training by utilizing a self-adaptive metric. Our framework combines multiple, diverse sampling distributions, each tailored to specific parameter gradients. This approach facilitates the importance sampling of vector-valued gradient estimation. Rather than naively combining multiple distributions, our framework involves optimally weighting data contribution across multiple distributions. This adapted combination of multiple importance yields superior gradient estimates, leading to faster training convergence. We demonstrate the effectiveness of our approach through empirical evaluations across a range of optimization tasks like classification and regression on both image and point cloud datasets.

Blue noise for diffusion models

Most of the existing diffusion models use Gaussian noise for training and sampling across all time steps, which may not optimally account for the frequency contents reconstructed by the denoising network. Despite the diverse applications of correlated noise in computer graphics, its potential for improving the training process has been underexplored. In this paper, we introduce a novel and general class of diffusion models taking correlated noise within and across images into account. More specifically, we propose a time-varying noise model to incorporate correlated noise into the training process, as well as a method for fast generation of correlated noise mask. Our model is built upon deterministic diffusion models and utilizes blue noise to help improve the generation quality compared to using Gaussian white (random) noise only. Further, our framework allows introducing correlation across images within a single mini-batch to improve gradient flow. We perform both qualitative and quantitative evaluations on a variety of datasets using our method, achieving improvements on different tasks over existing deterministic diffusion models in terms of FID metric.

Efficient Gradient Estimation via Adaptive Sampling and Importance Sampling

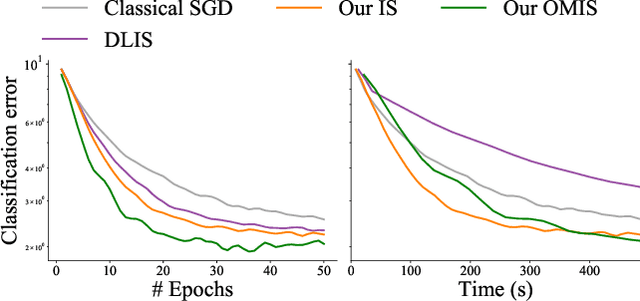
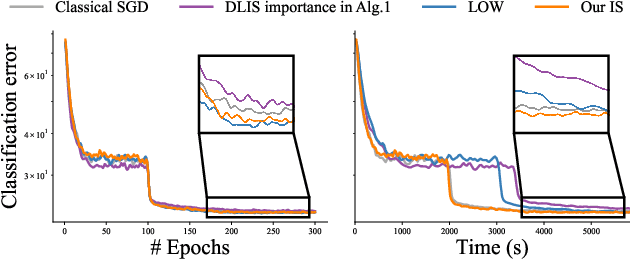
Machine learning problems rely heavily on stochastic gradient descent (SGD) for optimization. The effectiveness of SGD is contingent upon accurately estimating gradients from a mini-batch of data samples. Instead of the commonly used uniform sampling, adaptive or importance sampling reduces noise in gradient estimation by forming mini-batches that prioritize crucial data points. Previous research has suggested that data points should be selected with probabilities proportional to their gradient norm. Nevertheless, existing algorithms have struggled to efficiently integrate importance sampling into machine learning frameworks. In this work, we make two contributions. First, we present an algorithm that can incorporate existing importance functions into our framework. Second, we propose a simplified importance function that relies solely on the loss gradient of the output layer. By leveraging our proposed gradient estimation techniques, we observe improved convergence in classification and regression tasks with minimal computational overhead. We validate the effectiveness of our adaptive and importance-sampling approach on image and point-cloud datasets.