Convergence Analysis of Nonconvex Distributed Stochastic Zeroth-order Coordinate Method

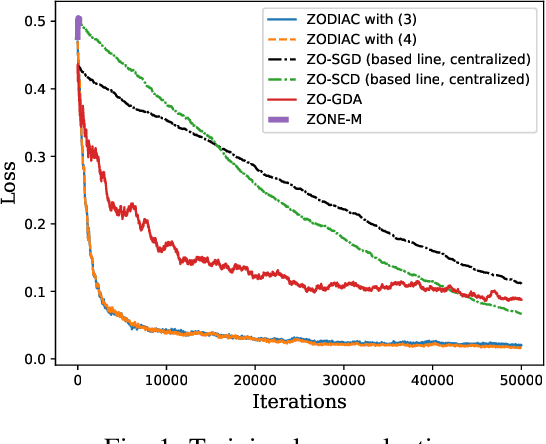
This paper investigates the stochastic distributed nonconvex optimization problem of minimizing a global cost function formed by the summation of $n$ local cost functions. We solve such a problem by involving zeroth-order (ZO) information exchange. In this paper, we propose a ZO distributed primal-dual coordinate method (ZODIAC) to solve the stochastic optimization problem. Agents approximate their own local stochastic ZO oracle along with coordinates with an adaptive smoothing parameter. We show that the proposed algorithm achieves the convergence rate of $\mathcal{O}(\sqrt{p}/\sqrt{T})$ for general nonconvex cost functions. We demonstrate the efficiency of proposed algorithms through a numerical example in comparison with the existing state-of-the-art centralized and distributed ZO algorithms.

Obstacle Avoidance and Navigation Utilizing Reinforcement Learning with Reward Shaping

In this paper, we investigate the obstacle avoidance and navigation problem in the robotic control area. For solving such a problem, we propose revised Deep Deterministic Policy Gradient (DDPG) and Proximal Policy Optimization algorithms with an improved reward shaping technique. We compare the performances between the original DDPG and PPO with the revised version of both on simulations with a real mobile robot and demonstrate that the proposed algorithms achieve better results.

Extremal Region Analysis based Deep Learning Framework for Detecting Defects

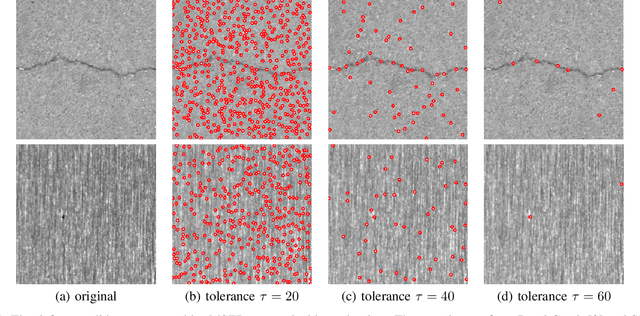
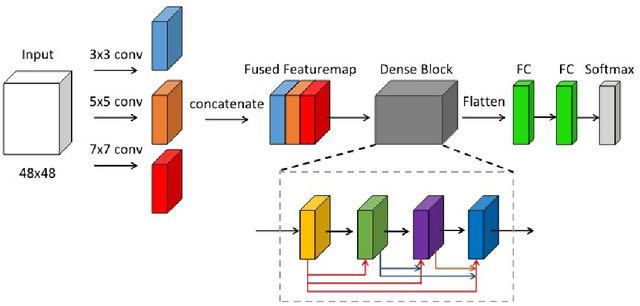
A maximally stable extreme region (MSER) analysis based convolutional neural network (CNN) for unified defect detection framework is proposed in this paper. Our proposed framework utilizes the generality and stability of MSER to generate the desired defect candidates. Then a specific trained binary CNN classifier is adopted over the defect candidates to produce the final defect set. Defect datasets over different categories \blue{are used} in the experiments. More generally, the parameter settings in MSER can be adjusted to satisfy different requirements in various industries (high precision, high recall, etc). Extensive experimental results have shown the efficacy of the proposed framework.