Convergence Analysis of Nonconvex Distributed Stochastic Zeroth-order Coordinate Method
Paper and Code
Mar 24, 2021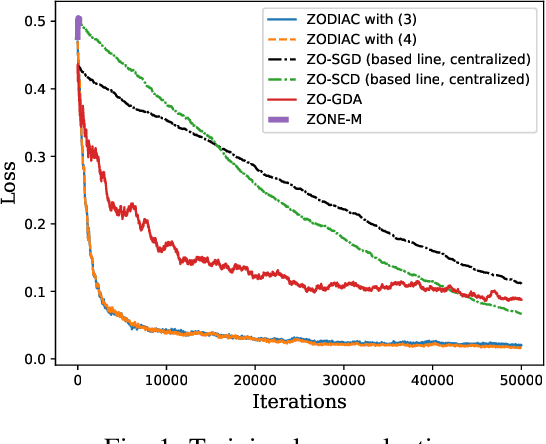


This paper investigates the stochastic distributed nonconvex optimization problem of minimizing a global cost function formed by the summation of $n$ local cost functions. We solve such a problem by involving zeroth-order (ZO) information exchange. In this paper, we propose a ZO distributed primal-dual coordinate method (ZODIAC) to solve the stochastic optimization problem. Agents approximate their own local stochastic ZO oracle along with coordinates with an adaptive smoothing parameter. We show that the proposed algorithm achieves the convergence rate of $\mathcal{O}(\sqrt{p}/\sqrt{T})$ for general nonconvex cost functions. We demonstrate the efficiency of proposed algorithms through a numerical example in comparison with the existing state-of-the-art centralized and distributed ZO algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge