Co-Correcting: Noise-tolerant Medical Image Classification via mutual Label Correction

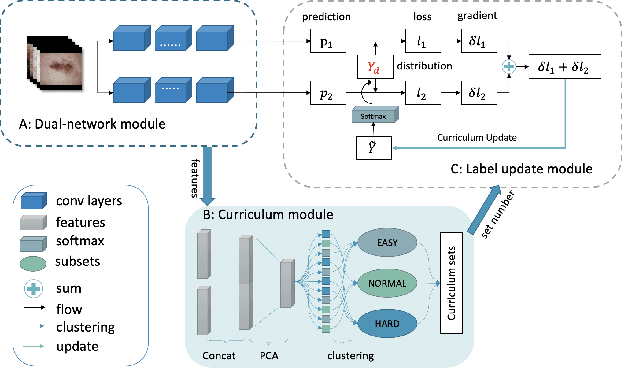
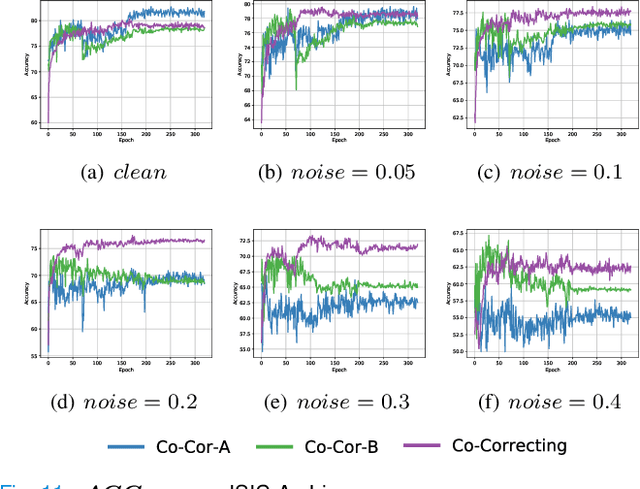
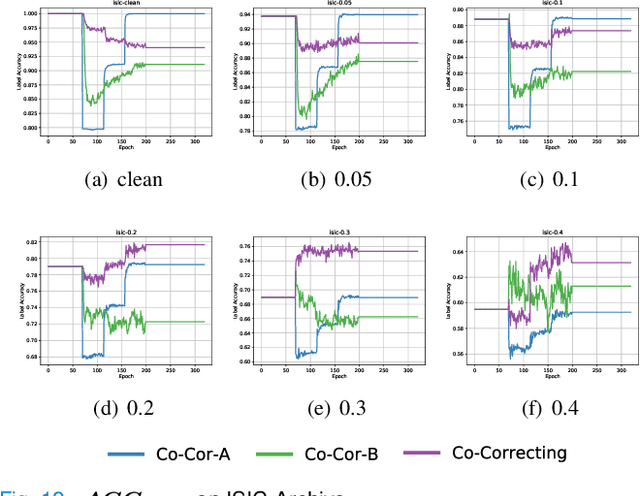
With the development of deep learning, medical image classification has been significantly improved. However, deep learning requires massive data with labels. While labeling the samples by human experts is expensive and time-consuming, collecting labels from crowd-sourcing suffers from the noises which may degenerate the accuracy of classifiers. Therefore, approaches that can effectively handle label noises are highly desired. Unfortunately, recent progress on handling label noise in deep learning has gone largely unnoticed by the medical image. To fill the gap, this paper proposes a noise-tolerant medical image classification framework named Co-Correcting, which significantly improves classification accuracy and obtains more accurate labels through dual-network mutual learning, label probability estimation, and curriculum label correcting. On two representative medical image datasets and the MNIST dataset, we test six latest Learning-with-Noisy-Labels methods and conduct comparative studies. The experiments show that Co-Correcting achieves the best accuracy and generalization under different noise ratios in various tasks. Our project can be found at: https://github.com/JiarunLiu/Co-Correcting.

DeFed: A Principled Decentralized and Privacy-Preserving Federated Learning Algorithm

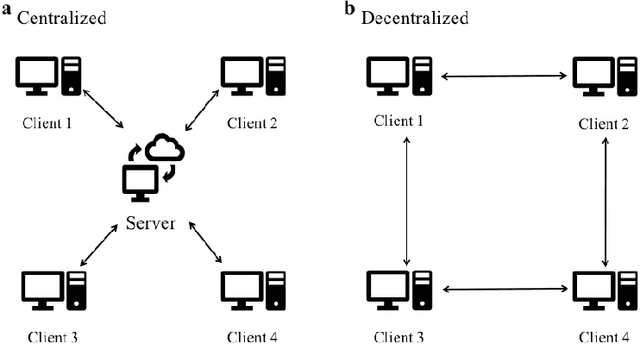
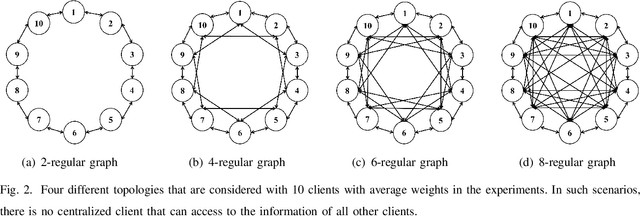
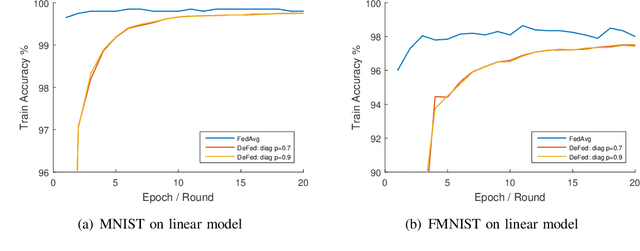
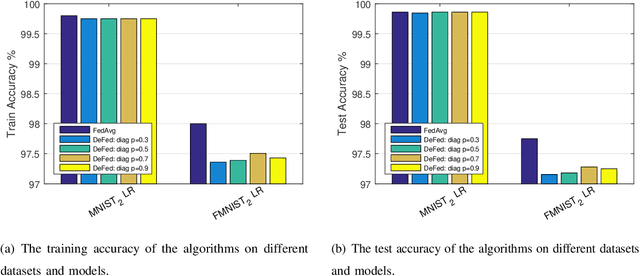
Federated learning enables a large number of clients to participate in learning a shared model while maintaining the training data stored in each client, which protects data privacy and security. Till now, federated learning frameworks are built in a centralized way, in which a central client is needed for collecting and distributing information from every other client. This not only leads to high communication pressure at the central client, but also renders the central client highly vulnerable to failure and attack. Here we propose a principled decentralized federated learning algorithm (DeFed), which removes the central client in the classical Federated Averaging (FedAvg) setting and only relies information transmission between clients and their local neighbors. The proposed DeFed algorithm is proven to reach the global minimum with a convergence rate of $O(1/T)$ when the loss function is smooth and strongly convex, where $T$ is the number of iterations in gradient descent. Finally, the proposed algorithm has been applied to a number of toy examples to demonstrate its effectiveness.