Christopher R. Aberger
Revisiting BFloat16 Training
Oct 13, 2020



Abstract:State-of-the-art generic low-precision training algorithms use a mix of 16-bit and 32-bit precision, creating the folklore that 16-bit precision alone is not enough to maximize model accuracy. As a result, deep learning accelerators are forced to support both 16-bit and 32-bit compute units which is more costly than only using 16-bit units for hardware design. We ask can we do pure 16-bit training which requires only 16-bit compute units, while still matching the model accuracy attained by 32-bit training. Towards this end, we study pure 16-bit training algorithms on the widely adopted BFloat16 compute unit. While these units conventionally use nearest rounding to cast output to 16-bit precision, we show that nearest rounding for model weight updates can often cancel small updates, which degrades the convergence and model accuracy. Motivated by this, we identify two simple existing techniques, stochastic rounding and Kahan summation, to remedy the model accuracy degradation in pure 16-bit training. We empirically show that these two techniques can enable up to 7% absolute validation accuracy gain in pure 16-bit training. This leads to 0.1% lower to 0.2% higher matching validation accuracy compared to 32-bit precision training across seven deep learning applications.
Understanding the Downstream Instability of Word Embeddings
Feb 29, 2020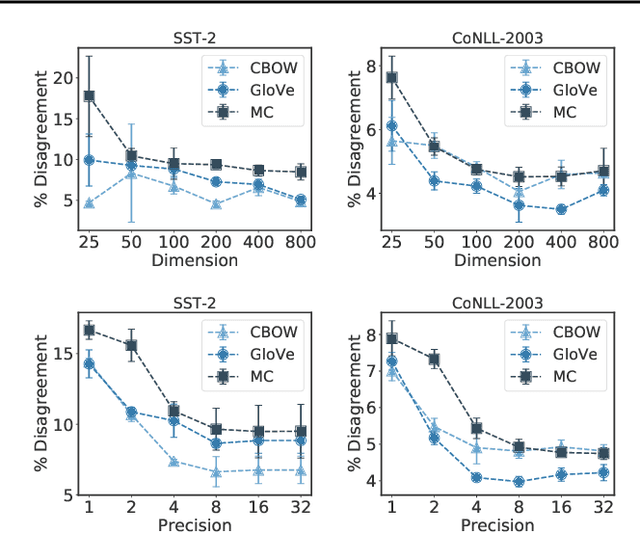

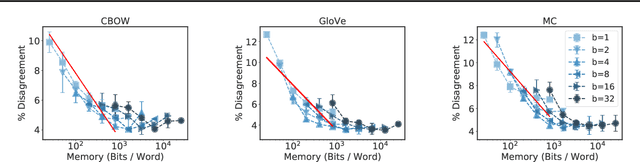
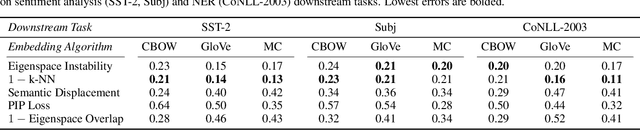
Abstract:Many industrial machine learning (ML) systems require frequent retraining to keep up-to-date with constantly changing data. This retraining exacerbates a large challenge facing ML systems today: model training is unstable, i.e., small changes in training data can cause significant changes in the model's predictions. In this paper, we work on developing a deeper understanding of this instability, with a focus on how a core building block of modern natural language processing (NLP) pipelines---pre-trained word embeddings---affects the instability of downstream NLP models. We first empirically reveal a tradeoff between stability and memory: increasing the embedding memory 2x can reduce the disagreement in predictions due to small changes in training data by 5% to 37% (relative). To theoretically explain this tradeoff, we introduce a new measure of embedding instability---the eigenspace instability measure---which we prove bounds the disagreement in downstream predictions introduced by the change in word embeddings. Practically, we show that the eigenspace instability measure can be a cost-effective way to choose embedding parameters to minimize instability without training downstream models, outperforming other embedding distance measures and performing competitively with a nearest neighbor-based measure. Finally, we demonstrate that the observed stability-memory tradeoffs extend to other types of embeddings as well, including knowledge graph and contextual word embeddings.
PipeMare: Asynchronous Pipeline Parallel DNN Training
Oct 09, 2019



Abstract:Recently there has been a flurry of interest around using pipeline parallelism while training neural networks. Pipeline parallelism enables larger models to be partitioned spatially across chips and within a chip, leading to both lower network communication and overall higher hardware utilization. Unfortunately, to preserve statistical efficiency, existing pipeline-parallelism techniques sacrifice hardware efficiency by introducing bubbles into the pipeline and/or incurring extra memory costs. In this paper, we investigate to what extent these sacrifices are necessary. Theoretically, we derive a simple but robust training method, called PipeMare, that tolerates asynchronous updates during pipeline-parallel execution. Using this, we show empirically, on a ResNet network and a Transformer network, that PipeMare can achieve final model qualities that match those of synchronous training techniques (at most 0.9% worse test accuracy and 0.3 better test BLEU score) while either using up to 2.0X less weight and optimizer memory or being up to 3.3X faster than other pipeline parallel training techniques. To the best of our knowledge we are the first to explore these techniques and fine-grained pipeline parallelism (e.g. the number of pipeline stages equals to the number of layers) during neural network training.
High-Accuracy Low-Precision Training
Mar 09, 2018

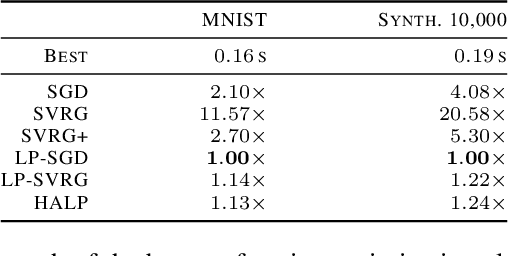

Abstract:Low-precision computation is often used to lower the time and energy cost of machine learning, and recently hardware accelerators have been developed to support it. Still, it has been used primarily for inference - not training. Previous low-precision training algorithms suffered from a fundamental tradeoff: as the number of bits of precision is lowered, quantization noise is added to the model, which limits statistical accuracy. To address this issue, we describe a simple low-precision stochastic gradient descent variant called HALP. HALP converges at the same theoretical rate as full-precision algorithms despite the noise introduced by using low precision throughout execution. The key idea is to use SVRG to reduce gradient variance, and to combine this with a novel technique called bit centering to reduce quantization error. We show that on the CPU, HALP can run up to $4 \times$ faster than full-precision SVRG and can match its convergence trajectory. We implemented HALP in TensorQuant, and show that it exceeds the validation performance of plain low-precision SGD on two deep learning tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge