Extrapolating tipping points and simulating non-stationary dynamics of complex systems using efficient machine learning

Model-free and data-driven prediction of tipping point transitions in nonlinear dynamical systems is a challenging and outstanding task in complex systems science. We propose a novel, fully data-driven machine learning algorithm based on next-generation reservoir computing to extrapolate the bifurcation behavior of nonlinear dynamical systems using stationary training data samples. We show that this method can extrapolate tipping point transitions. Furthermore, it is demonstrated that the trained next-generation reservoir computing architecture can be used to predict non-stationary dynamics with time-varying bifurcation parameters. In doing so, post-tipping point dynamics of unseen parameter regions can be simulated.

Forecasting Trends in Food Security: a Reservoir Computing Approach

Early warning systems are an essential tool for effective humanitarian action. Advance warnings on impending disasters facilitate timely and targeted response which help save lives, livelihoods, and scarce financial resources. In this work we present a new quantitative methodology to forecast levels of food consumption for 60 consecutive days, at the sub-national level, in four countries: Mali, Nigeria, Syria, and Yemen. The methodology is built on publicly available data from the World Food Programme's integrated global hunger monitoring system which collects, processes, and displays daily updates on key food security metrics, conflict, weather events, and other drivers of food insecurity across 90 countries (https://hungermap.wfp.org/). In this study, we assessed the performance of various models including ARIMA, XGBoost, LSTMs, CNNs, and Reservoir Computing (RC), by comparing their Root Mean Squared Error (RMSE) metrics. This comprehensive analysis spanned classical statistical, machine learning, and deep learning approaches. Our findings highlight Reservoir Computing as a particularly well-suited model in the field of food security given both its notable resistance to over-fitting on limited data samples and its efficient training capabilities. The methodology we introduce establishes the groundwork for a global, data-driven early warning system designed to anticipate and detect food insecurity.

Weight fluctuations in (deep) linear neural networks and a derivation of the inverse-variance flatness relation

We investigate the stationary (late-time) training regime of single- and two-layer linear neural networks within the continuum limit of stochastic gradient descent (SGD) for synthetic Gaussian data. In the case of a single-layer network in the weakly oversampled regime, the spectrum of the noise covariance matrix deviates notably from the Hessian, which can be attributed to the broken detailed balance of SGD dynamics. The weight fluctuations are in this case generally anisotropic, but experience an isotropic loss. For a two-layer network, we obtain the stochastic dynamics of the weights in each layer and analyze the associated stationary covariances. We identify the inter-layer coupling as a new source of anisotropy for the weight fluctuations. In contrast to the single-layer case, the weight fluctuations experience an anisotropic loss, the flatness of which is inversely related to the fluctuation variance. We thereby provide an analytical derivation of the recently observed inverse variance-flatness relation in a deep linear network model.

Controlling dynamical systems to complex target states using machine learning: next-generation vs. classical reservoir computing

Controlling nonlinear dynamical systems using machine learning allows to not only drive systems into simple behavior like periodicity but also to more complex arbitrary dynamics. For this, it is crucial that a machine learning system can be trained to reproduce the target dynamics sufficiently well. On the example of forcing a chaotic parametrization of the Lorenz system into intermittent dynamics, we show first that classical reservoir computing excels at this task. In a next step, we compare those results based on different amounts of training data to an alternative setup, where next-generation reservoir computing is used instead. It turns out that while delivering comparable performance for usual amounts of training data, next-generation RC significantly outperforms in situations where only very limited data is available. This opens even further practical control applications in real world problems where data is restricted.

Exploring the limits of multifunctionality across different reservoir computers

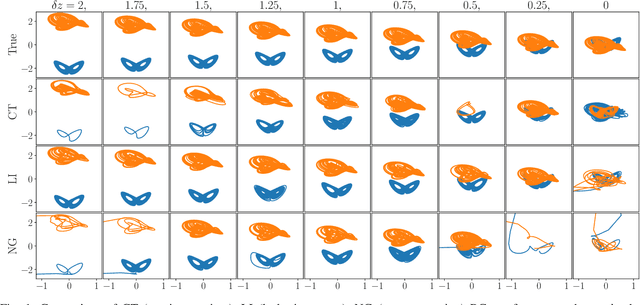
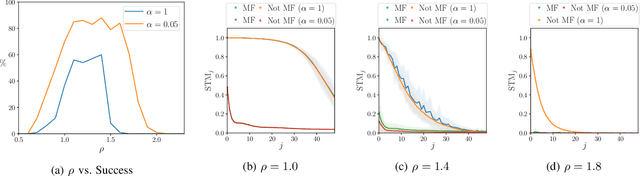
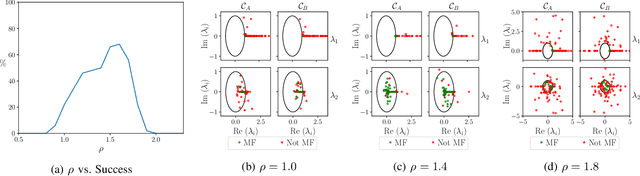
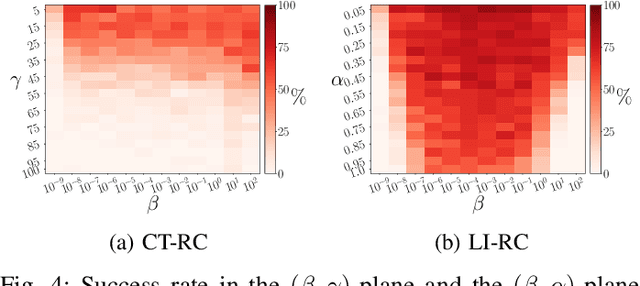
Multifunctional neural networks are capable of performing more than one task without changing any network connections. In this paper we explore the performance of a continuous-time, leaky-integrator, and next-generation `reservoir computer' (RC), when trained on tasks which test the limits of multifunctionality. In the first task we train each RC to reconstruct a coexistence of chaotic attractors from different dynamical systems. By moving the data describing these attractors closer together, we find that the extent to which each RC can reconstruct both attractors diminishes as they begin to overlap in state space. In order to provide a greater understanding of this inhibiting effect, in the second task we train each RC to reconstruct a coexistence of two circular orbits which differ only in the direction of rotation. We examine the critical effects that certain parameters can have in each RC to achieve multifunctionality in this extreme case of completely overlapping training data.

Controlling nonlinear dynamical systems into arbitrary states using machine learning

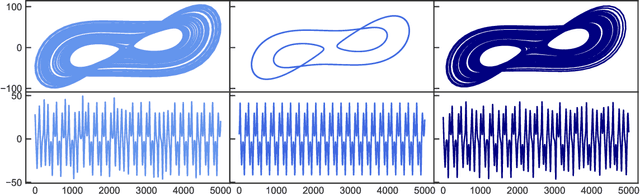
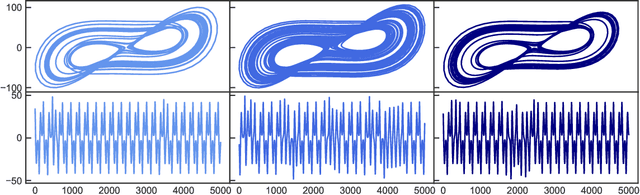
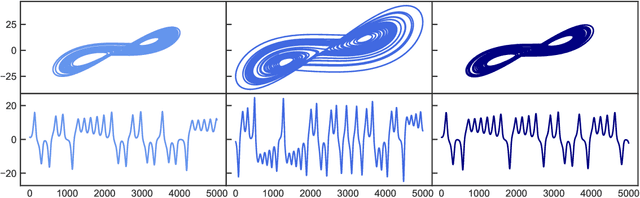
We propose a novel and fully data driven control scheme which relies on machine learning (ML). Exploiting recently developed ML-based prediction capabilities of complex systems, we demonstrate that nonlinear systems can be forced to stay in arbitrary dynamical target states coming from any initial state. We outline our approach using the examples of the Lorenz and the R\"ossler system and show how these systems can very accurately be brought not only to periodic but also to e.g. intermittent and different chaotic behavior. Having this highly flexible control scheme with little demands on the amount of required data on hand, we briefly discuss possible applications that range from engineering to medicine.

Reservoir Computing and its Sensitivity to Symmetry in the Activation Function

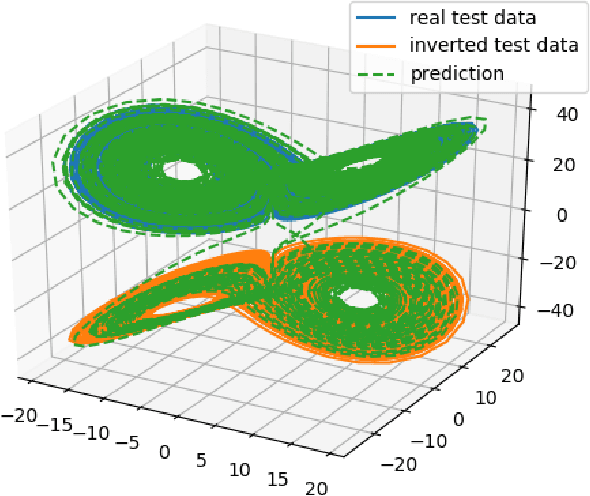
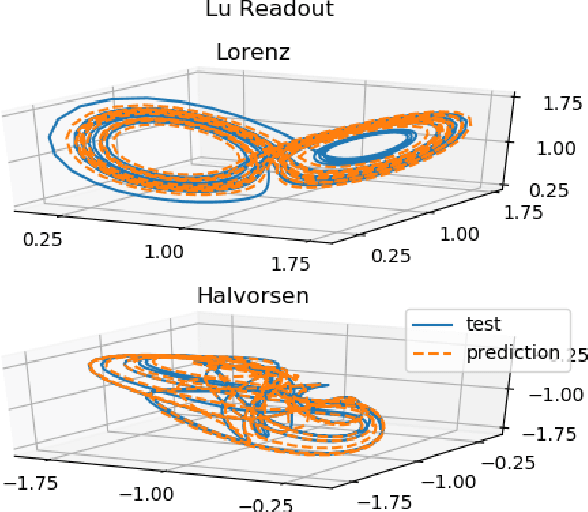
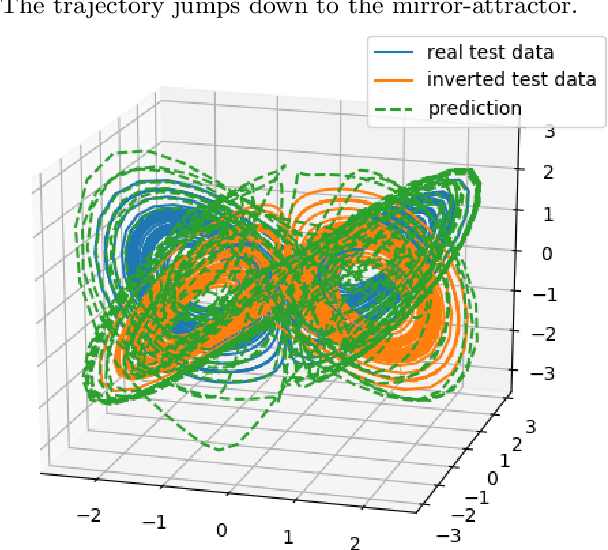
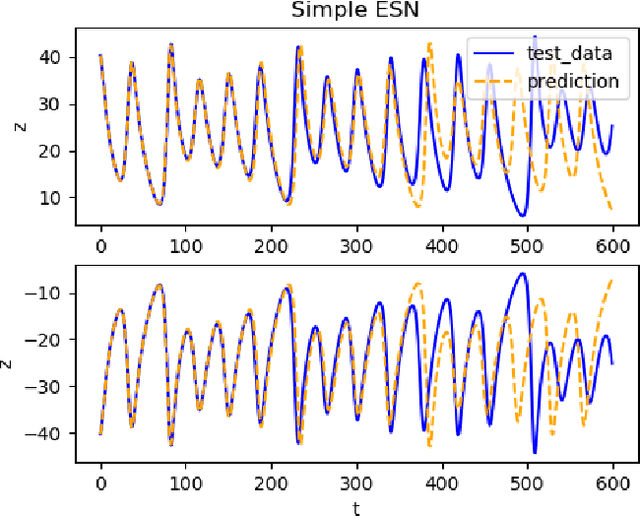
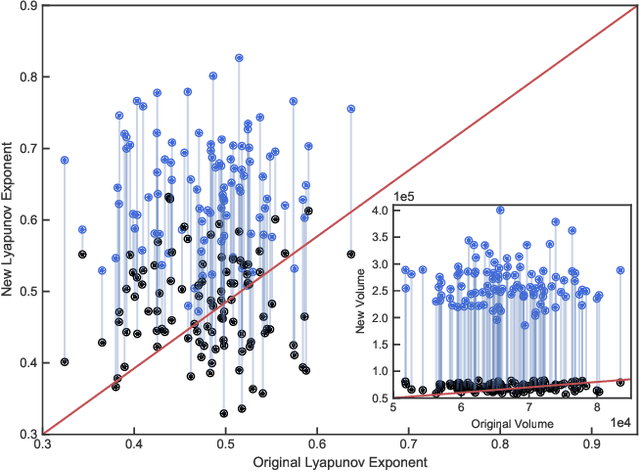
Reservoir computing has repeatedly been shown to be extremely successful in the prediction of nonlinear time-series. However, there is no complete understanding of the proper design of a reservoir yet. We find that the simplest popular setup has a harmful symmetry, which leads to the prediction of what we call mirror-attractor. We prove this analytically. Similar problems can arise in a general context, and we use them to explain the success or failure of some designs. The symmetry is a direct consequence of the hyperbolic tangent activation function. Further, four ways to break the symmetry are compared numerically: A bias in the output, a shift in the input, a quadratic term in the readout, and a mixture of even and odd activation functions. Firstly, we test their susceptibility to the mirror-attractor. Secondly, we evaluate their performance on the task of predicting Lorenz data with the mean shifted to zero. The short-time prediction is measured with the forecast horizon while the largest Lyapunov exponent and the correlation dimension are used to represent the climate. Finally, the same analysis is repeated on a combined dataset of the Lorenz attractor and the Halvorsen attractor, which we designed to reveal potential problems with symmetry. We find that all methods except the output bias are able to fully break the symmetry with input shift and quadratic readout performing the best overall.