Reservoir Computing and its Sensitivity to Symmetry in the Activation Function

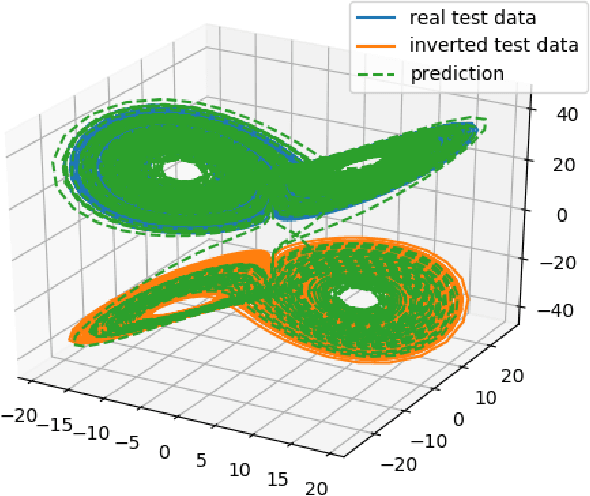
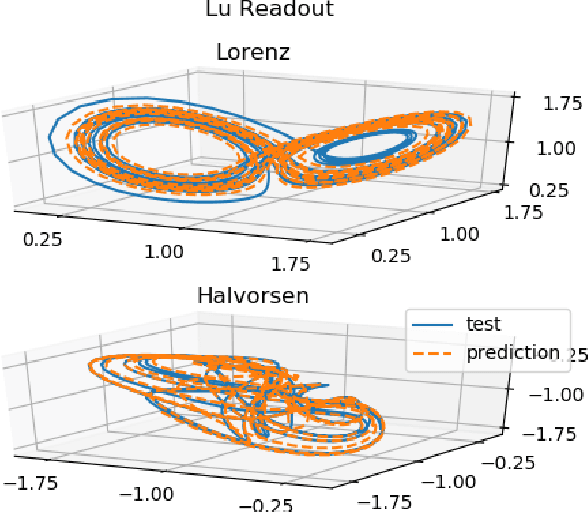
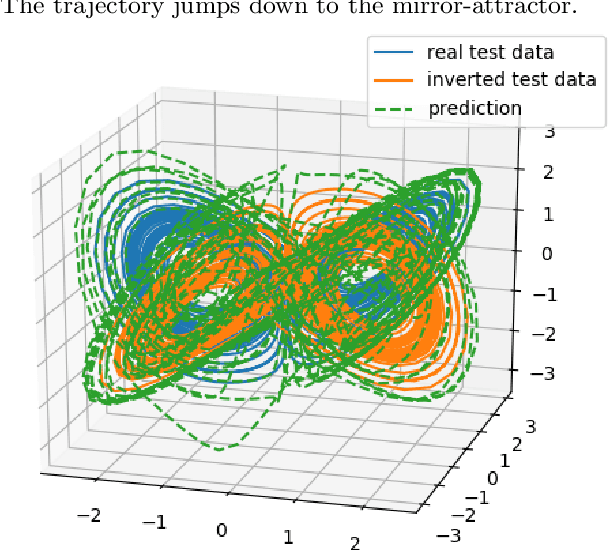
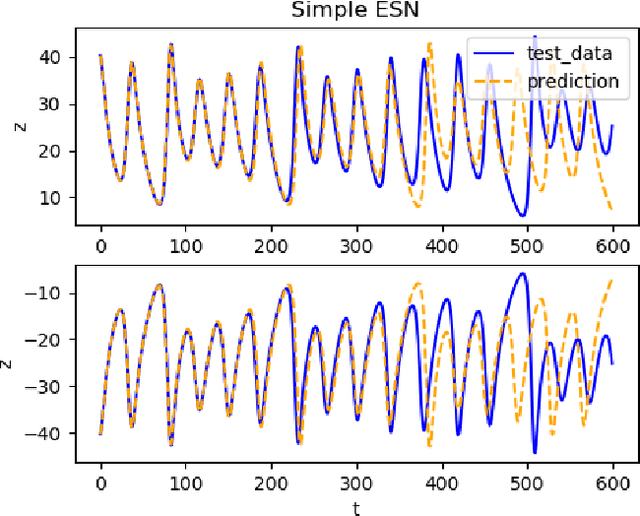
Reservoir computing has repeatedly been shown to be extremely successful in the prediction of nonlinear time-series. However, there is no complete understanding of the proper design of a reservoir yet. We find that the simplest popular setup has a harmful symmetry, which leads to the prediction of what we call mirror-attractor. We prove this analytically. Similar problems can arise in a general context, and we use them to explain the success or failure of some designs. The symmetry is a direct consequence of the hyperbolic tangent activation function. Further, four ways to break the symmetry are compared numerically: A bias in the output, a shift in the input, a quadratic term in the readout, and a mixture of even and odd activation functions. Firstly, we test their susceptibility to the mirror-attractor. Secondly, we evaluate their performance on the task of predicting Lorenz data with the mean shifted to zero. The short-time prediction is measured with the forecast horizon while the largest Lyapunov exponent and the correlation dimension are used to represent the climate. Finally, the same analysis is repeated on a combined dataset of the Lorenz attractor and the Halvorsen attractor, which we designed to reveal potential problems with symmetry. We find that all methods except the output bias are able to fully break the symmetry with input shift and quadratic readout performing the best overall.