Exploring the origins of switching dynamics in a multifunctional reservoir computer

The concept of multifunctionality has enabled reservoir computers (RCs), a type of dynamical system that is typically realised as an artificial neural network, to reconstruct multiple attractors simultaneously using the same set of trained weights. However there are many additional phenomena that arise when training a RC to reconstruct more than one attractor. Previous studies have found that, in certain cases, if the RC fails to reconstruct a coexistence of attractors then it exhibits a form of metastability whereby, without any external input, the state of the RC switches between different modes of behaviour that resemble properties of the attractors it failed to reconstruct. In this paper we explore the origins of these switching dynamics in a paradigmatic setting via the `seeing double' problem.

Multifunctionality in a Connectome-Based Reservoir Computer

Multifunctionality describes the capacity for a neural network to perform multiple mutually exclusive tasks without altering its network connections; and is an emerging area of interest in the reservoir computing machine learning paradigm. Multifunctionality has been observed in the brains of humans and other animals: particularly, in the lateral horn of the fruit fly. In this work, we transplant the connectome of the fruit fly lateral horn to a reservoir computer (RC), and investigate the extent to which this 'fruit fly RC' (FFRC) exhibits multifunctionality using the 'seeing double' problem as a benchmark test. We furthermore explore the dynamics of how this FFRC achieves multifunctionality while varying the network's spectral radius. Compared to the widely-used Erd\"os-Renyi Reservoir Computer (ERRC), we report that the FFRC exhibits a greater capacity for multifunctionality; is multifunctional across a broader hyperparameter range; and solves the seeing double problem far beyond the previously observed spectral radius limit, wherein the ERRC's dynamics become chaotic.

Seeing double with a multifunctional reservoir computer

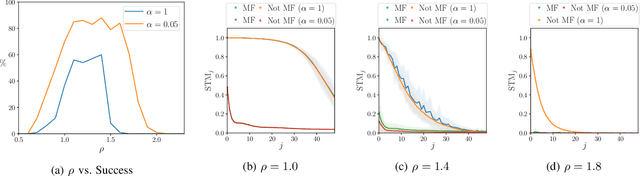
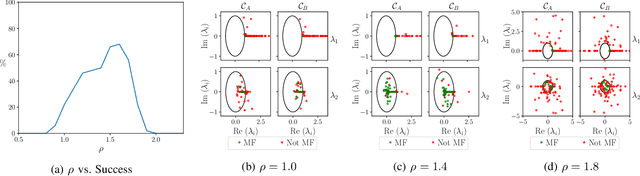
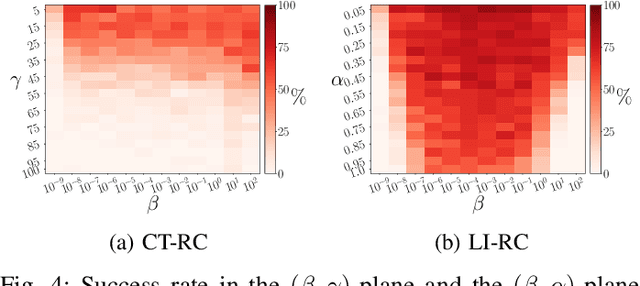
Multifunctional biological neural networks exploit multistability in order to perform multiple tasks without changing any network properties. Enabling artificial neural networks (ANNs) to obtain certain multistabilities in order to perform several tasks, where each task is related to a particular attractor in the network's state space, naturally has many benefits from a machine learning perspective. Given the association to multistability, in this paper we explore how the relationship between different attractors influences the ability of a reservoir computer (RC), which is a dynamical system in the form of an ANN, to achieve multifunctionality. We construct the `seeing double' problem to systematically study how a RC reconstructs a coexistence of attractors when there is an overlap between them. As the amount of overlap increases, we discover that for multifunctionality to occur, there is a critical dependence on a suitable choice of the spectral radius for the RC's internal network connections. A bifurcation analysis reveals how multifunctionality emerges and is destroyed as the RC enters a chaotic regime that can lead to chaotic itinerancy.

Exploring the limits of multifunctionality across different reservoir computers

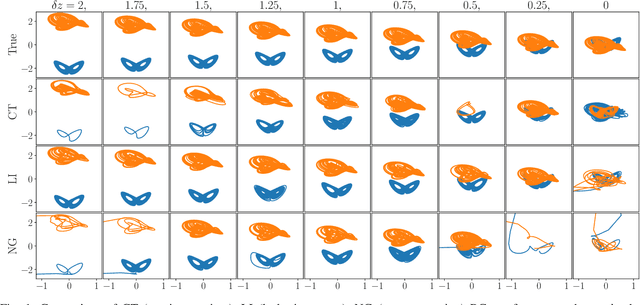
Multifunctional neural networks are capable of performing more than one task without changing any network connections. In this paper we explore the performance of a continuous-time, leaky-integrator, and next-generation `reservoir computer' (RC), when trained on tasks which test the limits of multifunctionality. In the first task we train each RC to reconstruct a coexistence of chaotic attractors from different dynamical systems. By moving the data describing these attractors closer together, we find that the extent to which each RC can reconstruct both attractors diminishes as they begin to overlap in state space. In order to provide a greater understanding of this inhibiting effect, in the second task we train each RC to reconstruct a coexistence of two circular orbits which differ only in the direction of rotation. We examine the critical effects that certain parameters can have in each RC to achieve multifunctionality in this extreme case of completely overlapping training data.

Multifunctionality in a Reservoir Computer

Multifunctionality is a well observed phenomenological feature of biological neural networks and considered to be of fundamental importance to the survival of certain species over time. These multifunctional neural networks are capable of performing more than one task without changing any network connections. In this paper we investigate how this neurological idiosyncrasy can be achieved in an artificial setting with a modern machine learning paradigm known as `Reservoir Computing'. A training technique is designed to enable a Reservoir Computer to perform tasks of a multifunctional nature. We explore the critical effects that changes in certain parameters can have on the Reservoir Computers' ability to express multifunctionality. We also expose the existence of several `untrained attractors'; attractors which dwell within the prediction state space of the Reservoir Computer that were not part of the training. We conduct a bifurcation analysis of these untrained attractors and discuss the implications of our results.