Oliver Heilmann
Exploring the limits of multifunctionality across different reservoir computers
May 23, 2022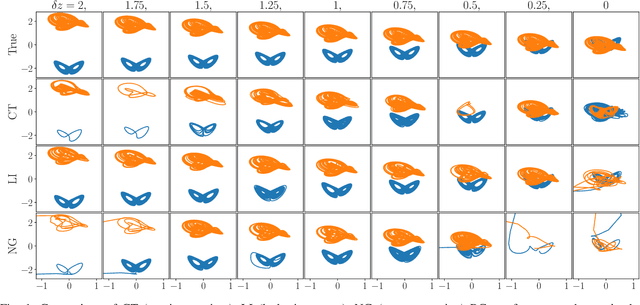
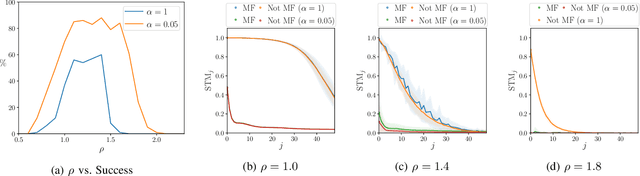
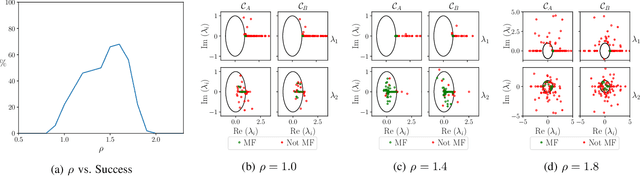
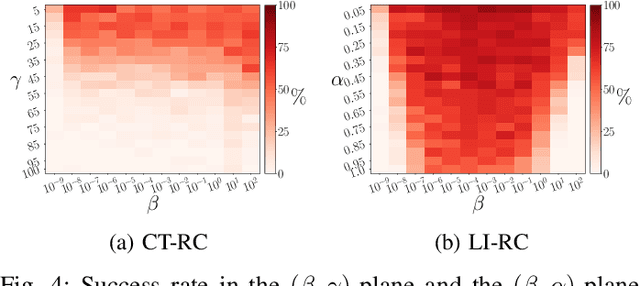
Abstract:Multifunctional neural networks are capable of performing more than one task without changing any network connections. In this paper we explore the performance of a continuous-time, leaky-integrator, and next-generation `reservoir computer' (RC), when trained on tasks which test the limits of multifunctionality. In the first task we train each RC to reconstruct a coexistence of chaotic attractors from different dynamical systems. By moving the data describing these attractors closer together, we find that the extent to which each RC can reconstruct both attractors diminishes as they begin to overlap in state space. In order to provide a greater understanding of this inhibiting effect, in the second task we train each RC to reconstruct a coexistence of two circular orbits which differ only in the direction of rotation. We examine the critical effects that certain parameters can have in each RC to achieve multifunctionality in this extreme case of completely overlapping training data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge