Multifunctionality in a Connectome-Based Reservoir Computer

Multifunctionality describes the capacity for a neural network to perform multiple mutually exclusive tasks without altering its network connections; and is an emerging area of interest in the reservoir computing machine learning paradigm. Multifunctionality has been observed in the brains of humans and other animals: particularly, in the lateral horn of the fruit fly. In this work, we transplant the connectome of the fruit fly lateral horn to a reservoir computer (RC), and investigate the extent to which this 'fruit fly RC' (FFRC) exhibits multifunctionality using the 'seeing double' problem as a benchmark test. We furthermore explore the dynamics of how this FFRC achieves multifunctionality while varying the network's spectral radius. Compared to the widely-used Erd\"os-Renyi Reservoir Computer (ERRC), we report that the FFRC exhibits a greater capacity for multifunctionality; is multifunctional across a broader hyperparameter range; and solves the seeing double problem far beyond the previously observed spectral radius limit, wherein the ERRC's dynamics become chaotic.

Using Connectome Features to Constrain Echo State Networks

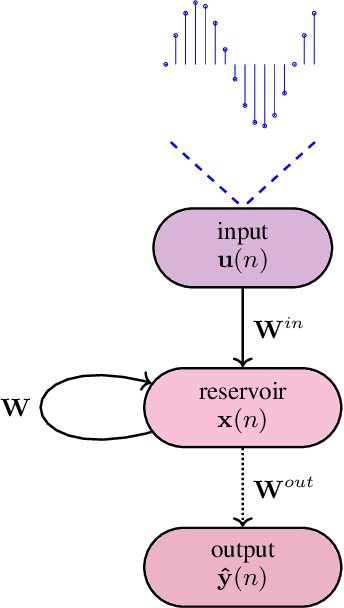
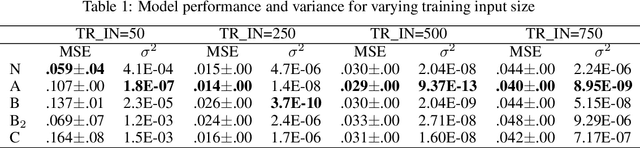
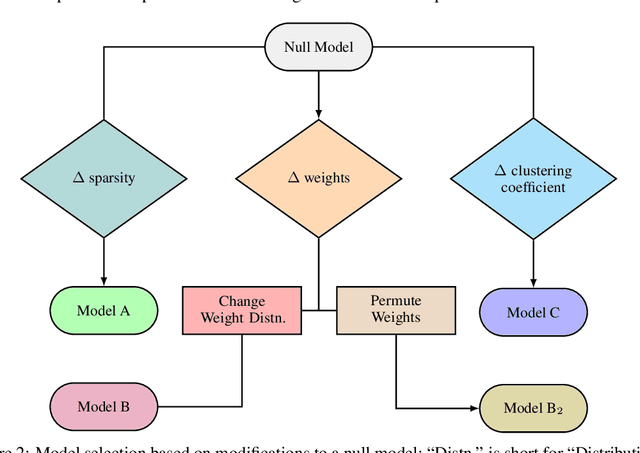
We report an improvement to the conventional Echo State Network (ESN), which already achieves competitive performance in one-dimensional time series prediction of dynamical systems. Our model -- a 20$\%$-dense ESN with reservoir weights derived from a fruit fly connectome (and from its bootstrapped distribution) -- yields superior performance on a chaotic time series prediction task, and furthermore alleviates the ESN's high-variance problem. We also find that an arbitrary positioning of weights can degrade ESN performance and variance; and that this can be remedied in particular by employing connectome-derived weight positions. Herein we consider four connectome features -- namely, the sparsity, positioning, distribution, and clustering of weights -- and construct corresponding model classes (A, B, B${}_2$, C) from an appropriate null model ESN; one with its reservoir layer replaced by a fruit fly connectivity matrix. After tuning relevant hyperparameters and selecting the best instance of each model class, we train and validate all models for multi-step prediction on size-variants (50, 250, 500, and 750 training input steps) of the Mackey-Glass chaotic time series; and compute their performance (Mean-Squared Error) and variance across train-validate trials.

Imposing Connectome-Derived Topology on an Echo State Network

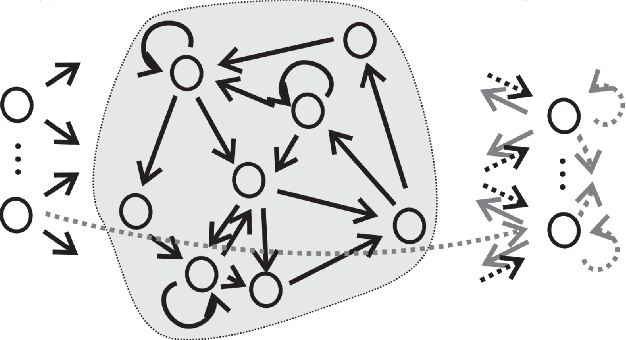
Can connectome-derived constraints inform computation? In this paper we investigate the contribution of a fruit fly connectome's topology on the performance of an Echo State Network (ESN) -- a subset of Reservoir Computing which is state of the art in chaotic time series prediction. Specifically, we replace the reservoir layer of a classical ESN -- normally a fixed, random graph represented as a 2-d matrix -- with a particular (female) fruit fly connectome-derived connectivity matrix. We refer to this experimental class of models (with connectome-derived reservoirs) as "Fruit Fly ESNs" (FFESNs). We train and validate the FFESN on a chaotic time series prediction task; here we consider four sets of trials with different training input sizes (small, large) and train-validate splits (two variants). We compare the validation performance (Mean-Squared Error) of all of the best FFESN models to a class of control model ESNs (simply referred to as "ESNs"). Overall, for all four sets of trials we find that the FFESN either significantly outperforms (and has lower variance than) the ESN; or simply has lower variance than the ESN.