Using Connectome Features to Constrain Echo State Networks

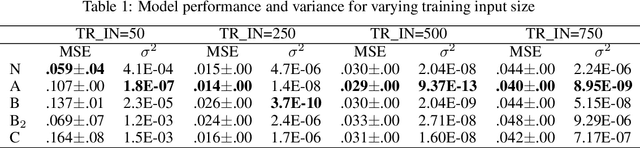
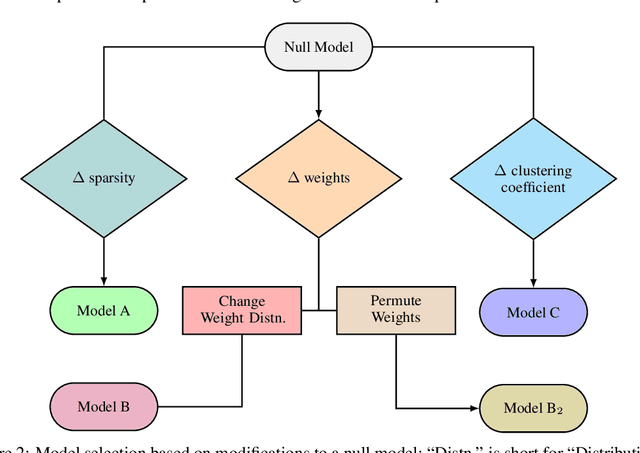
We report an improvement to the conventional Echo State Network (ESN), which already achieves competitive performance in one-dimensional time series prediction of dynamical systems. Our model -- a 20$\%$-dense ESN with reservoir weights derived from a fruit fly connectome (and from its bootstrapped distribution) -- yields superior performance on a chaotic time series prediction task, and furthermore alleviates the ESN's high-variance problem. We also find that an arbitrary positioning of weights can degrade ESN performance and variance; and that this can be remedied in particular by employing connectome-derived weight positions. Herein we consider four connectome features -- namely, the sparsity, positioning, distribution, and clustering of weights -- and construct corresponding model classes (A, B, B${}_2$, C) from an appropriate null model ESN; one with its reservoir layer replaced by a fruit fly connectivity matrix. After tuning relevant hyperparameters and selecting the best instance of each model class, we train and validate all models for multi-step prediction on size-variants (50, 250, 500, and 750 training input steps) of the Mackey-Glass chaotic time series; and compute their performance (Mean-Squared Error) and variance across train-validate trials.