Controlling dynamical systems into unseen target states using machine learning

We present a novel, model-free, and data-driven methodology for controlling complex dynamical systems into previously unseen target states, including those with significantly different and complex dynamics. Leveraging a parameter-aware realization of next-generation reservoir computing, our approach accurately predicts system behavior in unobserved parameter regimes, enabling control over transitions to arbitrary target states. Crucially, this includes states with dynamics that differ fundamentally from known regimes, such as shifts from periodic to intermittent or chaotic behavior. The method's parameter-awareness facilitates non-stationary control, ensuring smooth transitions between states. By extending the applicability of machine learning-based control mechanisms to previously inaccessible target dynamics, this methodology opens the door to transformative new applications while maintaining exceptional efficiency. Our results highlight reservoir computing as a powerful alternative to traditional methods for dynamic system control.

Controlling dynamical systems to complex target states using machine learning: next-generation vs. classical reservoir computing

Controlling nonlinear dynamical systems using machine learning allows to not only drive systems into simple behavior like periodicity but also to more complex arbitrary dynamics. For this, it is crucial that a machine learning system can be trained to reproduce the target dynamics sufficiently well. On the example of forcing a chaotic parametrization of the Lorenz system into intermittent dynamics, we show first that classical reservoir computing excels at this task. In a next step, we compare those results based on different amounts of training data to an alternative setup, where next-generation reservoir computing is used instead. It turns out that while delivering comparable performance for usual amounts of training data, next-generation RC significantly outperforms in situations where only very limited data is available. This opens even further practical control applications in real world problems where data is restricted.

Controlling nonlinear dynamical systems into arbitrary states using machine learning

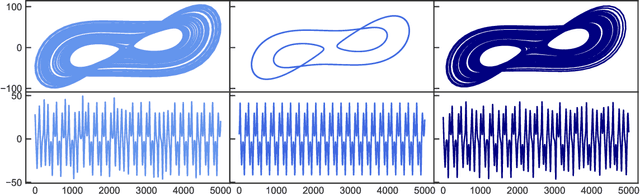
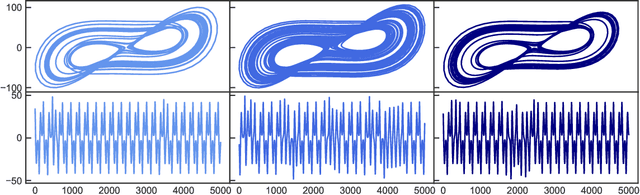
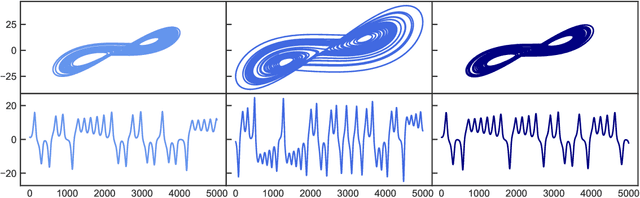
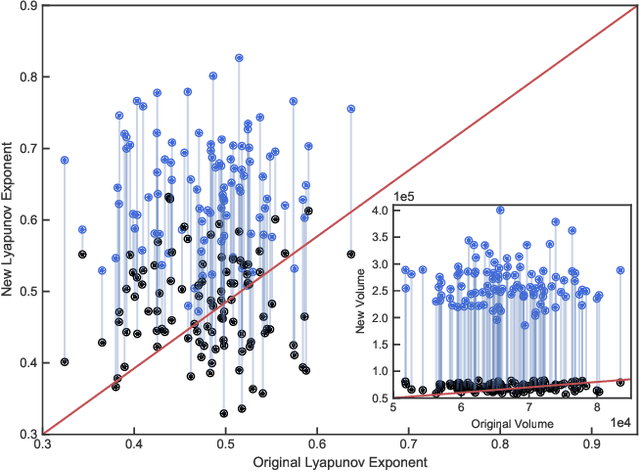
We propose a novel and fully data driven control scheme which relies on machine learning (ML). Exploiting recently developed ML-based prediction capabilities of complex systems, we demonstrate that nonlinear systems can be forced to stay in arbitrary dynamical target states coming from any initial state. We outline our approach using the examples of the Lorenz and the R\"ossler system and show how these systems can very accurately be brought not only to periodic but also to e.g. intermittent and different chaotic behavior. Having this highly flexible control scheme with little demands on the amount of required data on hand, we briefly discuss possible applications that range from engineering to medicine.