On the Convergence of Discounted Policy Gradient Methods

Many popular policy gradient methods for reinforcement learning follow a biased approximation of the policy gradient known as the discounted approximation. While it has been shown that the discounted approximation of the policy gradient is not the gradient of any objective function, little else is known about its convergence behavior or properties. In this paper, we show that if the discounted approximation is followed such that the discount factor is increased slowly at a rate related to a decreasing learning rate, the resulting method recovers the standard guarantees of gradient ascent on the undiscounted objective.

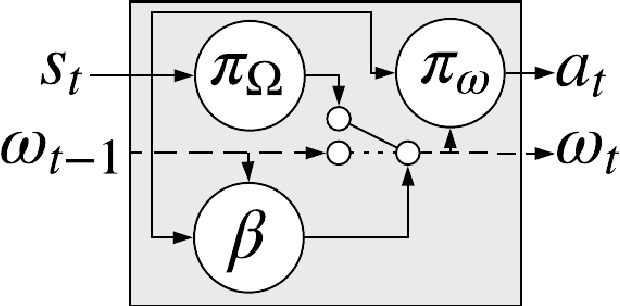
Learning Reusable Options for Multi-Task Reinforcement Learning

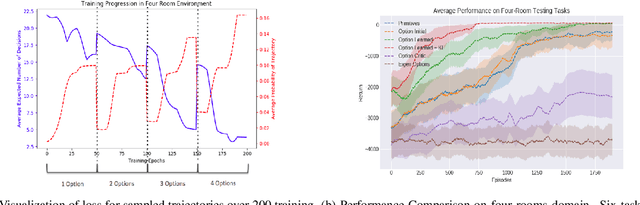
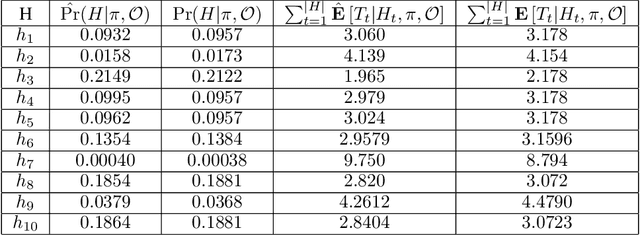
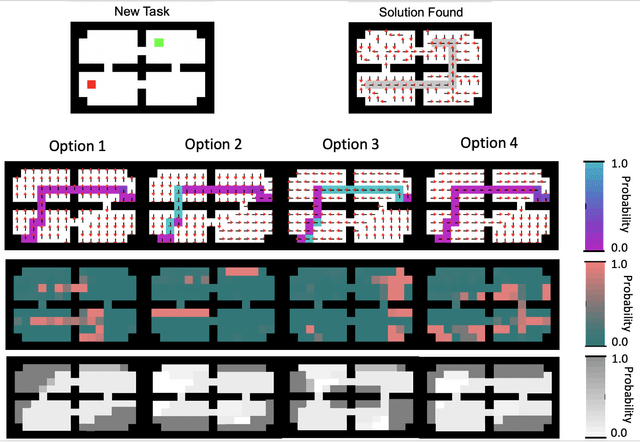
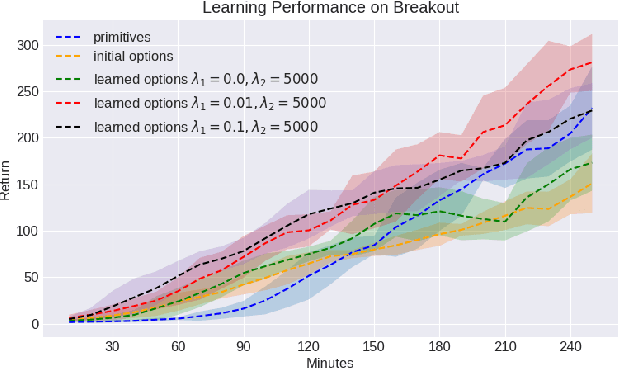
Reinforcement learning (RL) has become an increasingly active area of research in recent years. Although there are many algorithms that allow an agent to solve tasks efficiently, they often ignore the possibility that prior experience related to the task at hand might be available. For many practical applications, it might be unfeasible for an agent to learn how to solve a task from scratch, given that it is generally a computationally expensive process; however, prior experience could be leveraged to make these problems tractable in practice. In this paper, we propose a framework for exploiting existing experience by learning reusable options. We show that after an agent learns policies for solving a small number of problems, we are able to use the trajectories generated from those policies to learn reusable options that allow an agent to quickly learn how to solve novel and related problems.

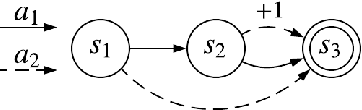
Is the Policy Gradient a Gradient?

The policy gradient theorem describes the gradient of the expected discounted return with respect to an agent's policy parameters. However, most policy gradient methods do not use the discount factor in the manner originally prescribed, and therefore do not optimize the discounted objective. It has been an open question in RL as to which, if any, objective they optimize instead. We show that the direction followed by these methods is not the gradient of any objective, and reclassify them as semi-gradient methods with respect to the undiscounted objective. Further, we show that they are not guaranteed to converge to a locally optimal policy, and construct an counterexample where they will converge to the globally pessimal policy with respect to both the discounted and undiscounted objectives.

Classical Policy Gradient: Preserving Bellman's Principle of Optimality

We propose a new objective function for finite-horizon episodic Markov decision processes that better captures Bellman's principle of optimality, and provide an expression for the gradient of the objective.

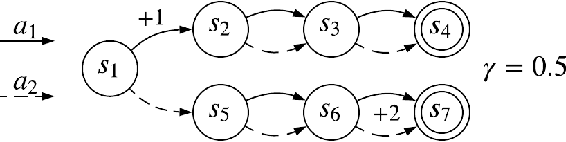
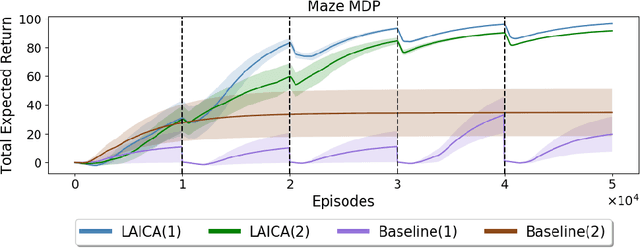
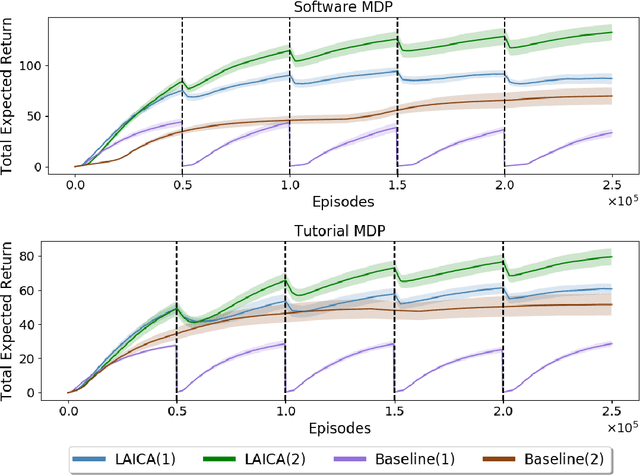
Lifelong Learning with a Changing Action Set

In many real-world sequential decision making problems, the number of available actions (decisions) can vary over time. While problems like catastrophic forgetting, changing transition dynamics, changing rewards functions, etc. have been well-studied in the lifelong learning literature, the setting where the action set changes remains unaddressed. In this paper, we present an algorithm that autonomously adapts to an action set whose size changes over time. To tackle this open problem, we break it into two problems that can be solved iteratively: inferring the underlying, unknown, structure in the space of actions and optimizing a policy that leverages this structure. We demonstrate the efficiency of this approach on large-scale real-world lifelong learning problems.

Asynchronous Coagent Networks: Stochastic Networks for Reinforcement Learning without Backpropagation or a Clock

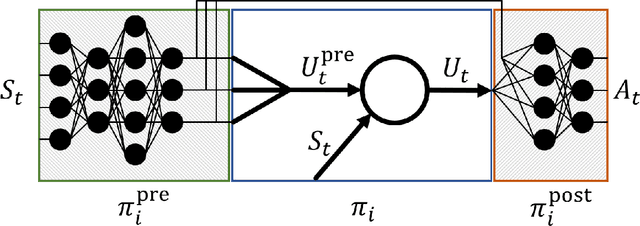
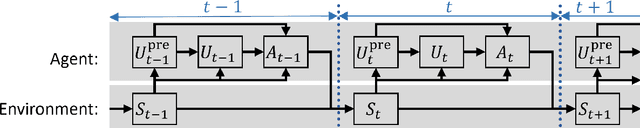
In this paper we introduce a reinforcement learning (RL) approach for training policies, including artificial neural network policies, that is both backpropagation-free and clock-free. It is backpropagation-free in that it does not propagate any information backwards through the network. It is clock-free in that no signal is given to each node in the network to specify when it should compute its output and when it should update its weights. We contend that these two properties increase the biological plausibility of our algorithms and facilitate distributed implementations. Additionally, our approach eliminates the need for customized learning rules for hierarchical RL algorithms like the option-critic.