Is the Policy Gradient a Gradient?

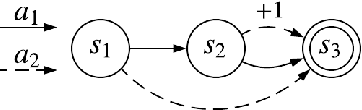
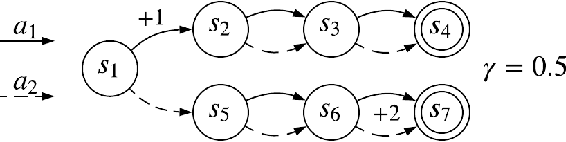
The policy gradient theorem describes the gradient of the expected discounted return with respect to an agent's policy parameters. However, most policy gradient methods do not use the discount factor in the manner originally prescribed, and therefore do not optimize the discounted objective. It has been an open question in RL as to which, if any, objective they optimize instead. We show that the direction followed by these methods is not the gradient of any objective, and reclassify them as semi-gradient methods with respect to the undiscounted objective. Further, we show that they are not guaranteed to converge to a locally optimal policy, and construct an counterexample where they will converge to the globally pessimal policy with respect to both the discounted and undiscounted objectives.