Regularized Adaptive Momentum Dual Averaging with an Efficient Inexact Subproblem Solver for Training Structured Neural Network

We propose a Regularized Adaptive Momentum Dual Averaging (RAMDA) algorithm for training structured neural networks. Similar to existing regularized adaptive methods, the subproblem for computing the update direction of RAMDA involves a nonsmooth regularizer and a diagonal preconditioner, and therefore does not possess a closed-form solution in general. We thus also carefully devise an implementable inexactness condition that retains convergence guarantees similar to the exact versions, and propose a companion efficient solver for the subproblems of both RAMDA and existing methods to make them practically feasible. We leverage the theory of manifold identification in variational analysis to show that, even in the presence of such inexactness, the iterates of RAMDA attain the ideal structure induced by the regularizer at the stationary point of asymptotic convergence. This structure is locally optimal near the point of convergence, so RAMDA is guaranteed to obtain the best structure possible among all methods converging to the same point, making it the first regularized adaptive method outputting models that possess outstanding predictive performance while being (locally) optimally structured. Extensive numerical experiments in large-scale modern computer vision, language modeling, and speech tasks show that the proposed RAMDA is efficient and consistently outperforms state of the art for training structured neural network. Implementation of our algorithm is available at http://www.github.com/ismoptgroup/RAMDA/.

Escaping Spurious Local Minima of Low-Rank Matrix Factorization Through Convex Lifting

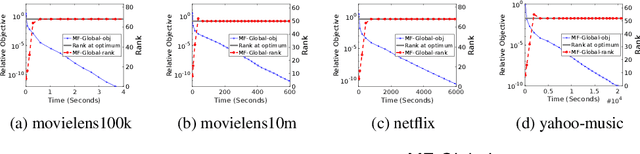
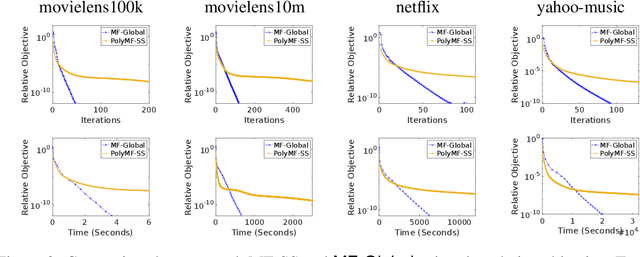
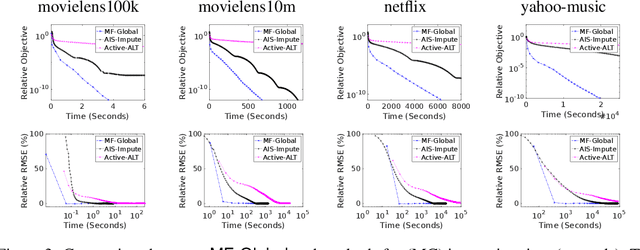
This work proposes a rapid global solver for nonconvex low-rank matrix factorization (MF) problems that we name MF-Global. Through convex lifting steps, our method efficiently escapes saddle points and spurious local minima ubiquitous in noisy real-world data, and is guaranteed to always converge to the global optima. Moreover, the proposed approach adaptively adjusts the rank for the factorization and provably identifies the optimal rank for MF automatically in the course of optimization through tools of manifold identification, and thus it also spends significantly less time on parameter tuning than existing MF methods, which require an exhaustive search for this optimal rank. On the other hand, when compared to methods for solving the lifted convex form only, MF-Global leads to significantly faster convergence and much shorter running time. Experiments on real-world large-scale recommendation system problems confirm that MF-Global can indeed effectively escapes spurious local solutions at which existing MF approaches stuck, and is magnitudes faster than state-of-the-art algorithms for the lifted convex form.

Training Structured Neural Networks Through Manifold Identification and Variance Reduction

This paper proposes an algorithm (RMDA) for training neural networks (NNs) with a regularization term for promoting desired structures. RMDA does not incur computation additional to proximal SGD with momentum, and achieves variance reduction without requiring the objective function to be of the finite-sum form. Through the tool of manifold identification from nonlinear optimization, we prove that after a finite number of iterations, all iterates of RMDA possess a desired structure identical to that induced by the regularizer at the stationary point of asymptotic convergence, even in the presence of engineering tricks like data augmentation and dropout that complicate the training process. Experiments on training NNs with structured sparsity confirm that variance reduction is necessary for such an identification, and show that RMDA thus significantly outperforms existing methods for this task. For unstructured sparsity, RMDA also outperforms a state-of-the-art pruning method, validating the benefits of training structured NNs through regularization.

A Distributed Quasi-Newton Algorithm for Primal and Dual Regularized Empirical Risk Minimization

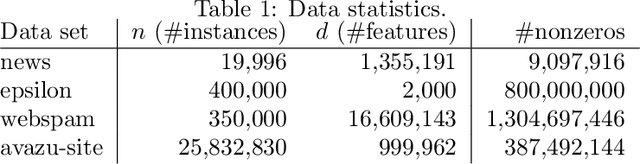
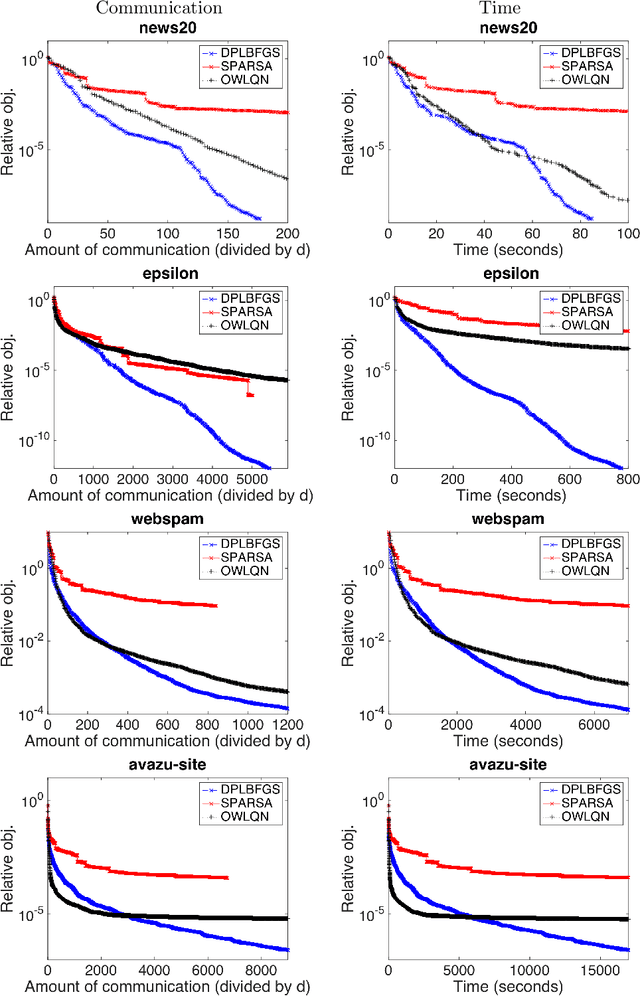
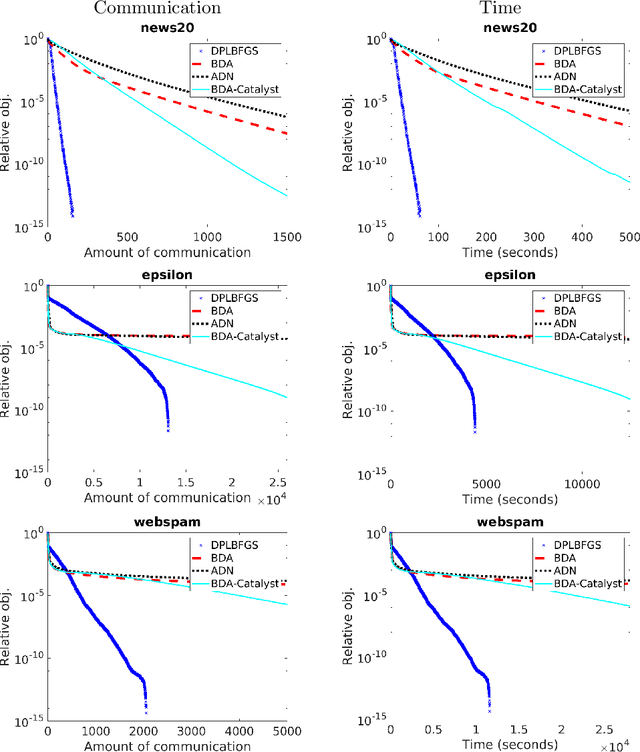
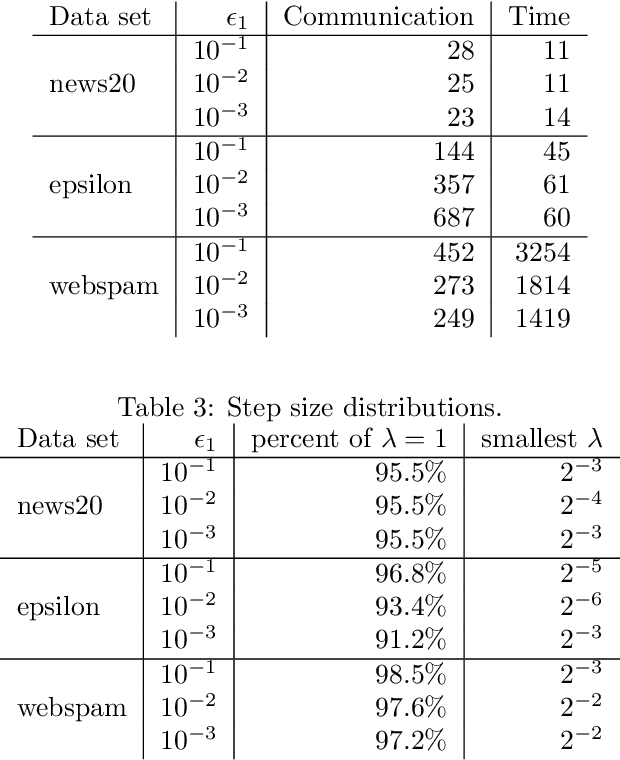
We propose a communication- and computation-efficient distributed optimization algorithm using second-order information for solving empirical risk minimization (ERM) problems with a nonsmooth regularization term. Our algorithm is applicable to both the primal and the dual ERM problem. Current second-order and quasi-Newton methods for this problem either do not work well in the distributed setting or work only for specific regularizers. Our algorithm uses successive quadratic approximations of the smooth part, and we describe how to maintain an approximation of the (generalized) Hessian and solve subproblems efficiently in a distributed manner. When applied to the distributed dual ERM problem, unlike state of the art that takes only the block-diagonal part of the Hessian, our approach is able to utilize global curvature information and is thus magnitudes faster. The proposed method enjoys global linear convergence for a broad range of non-strongly convex problems that includes the most commonly used ERMs, thus requiring lower communication complexity. It also converges on non-convex problems, so has the potential to be used on applications such as deep learning. Computational results demonstrate that our method significantly improves on communication cost and running time over the current state-of-the-art methods.

A Distributed Quasi-Newton Algorithm for Empirical Risk Minimization with Nonsmooth Regularization

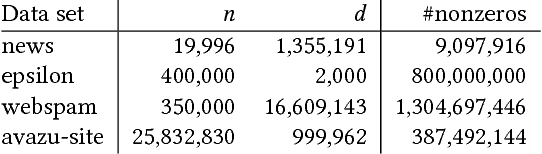
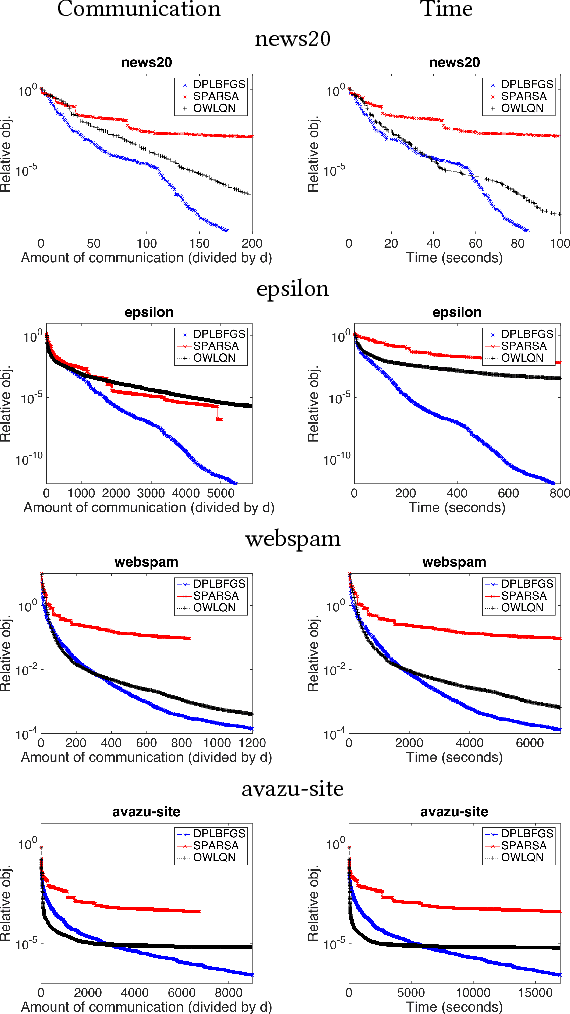
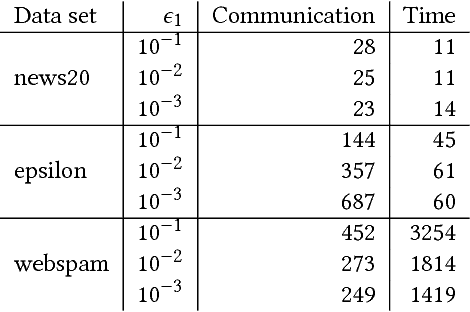
We propose a communication- and computation-efficient distributed optimization algorithm using second-order information for solving ERM problems with a nonsmooth regularization term. Current second-order and quasi-Newton methods for this problem either do not work well in the distributed setting or work only for specific regularizers. Our algorithm uses successive quadratic approximations, and we describe how to maintain an approximation of the Hessian and solve subproblems efficiently in a distributed manner. The proposed method enjoys global linear convergence for a broad range of non-strongly convex problems that includes the most commonly used ERMs, thus requiring lower communication complexity. It also converges on non-convex problems, so has the potential to be used on applications such as deep learning. Initial computational results on convex problems demonstrate that our method significantly improves on communication cost and running time over the current state-of-the-art methods.

Distributed Training of Structured SVM

Training structured prediction models is time-consuming. However, most existing approaches only use a single machine, thus, the advantage of computing power and the capacity for larger data sets of multiple machines have not been exploited. In this work, we propose an efficient algorithm for distributedly training structured support vector machines based on a distributed block-coordinate descent method. Both theoretical and experimental results indicate that our method is efficient.

On the Equivalence of CoCoA+ and DisDCA

In this document, we show that the algorithm CoCoA+ (Ma et al., ICML, 2015) under the setting used in their experiments, which is also the best setting suggested by the authors that proposed this algorithm, is equivalent to the practical variant of DisDCA (Yang, NIPS, 2013).