Hierarchical Verification for Adversarial Robustness

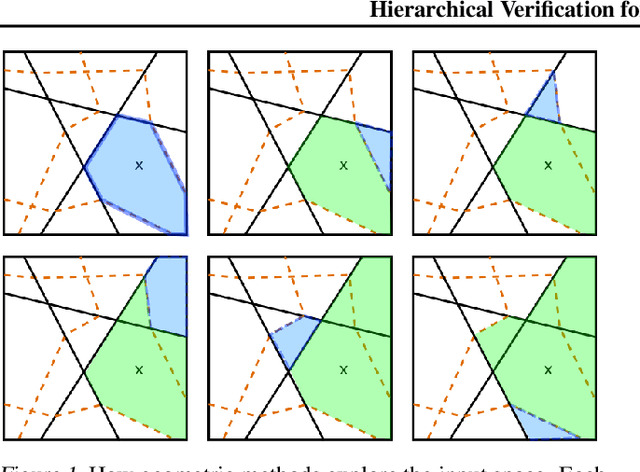
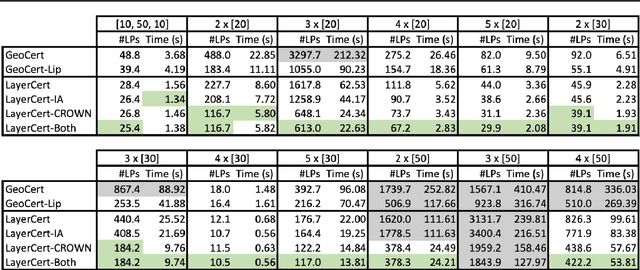
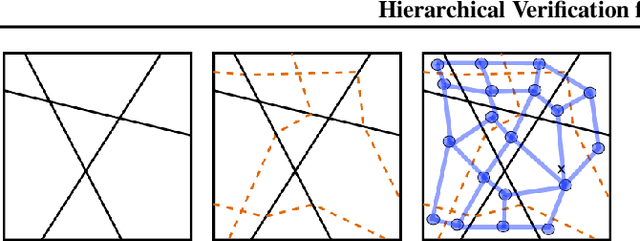
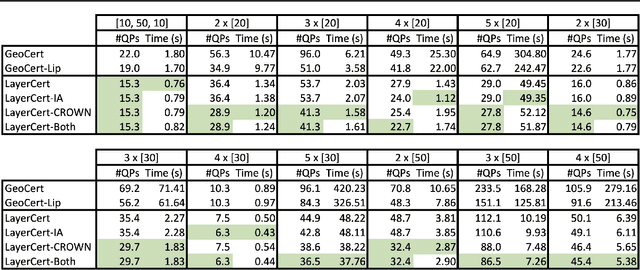
We introduce a new framework for the exact point-wise $\ell_p$ robustness verification problem that exploits the layer-wise geometric structure of deep feed-forward networks with rectified linear activations (ReLU networks). The activation regions of the network partition the input space, and one can verify the $\ell_p$ robustness around a point by checking all the activation regions within the desired radius. The GeoCert algorithm (Jordan et al., NeurIPS 2019) treats this partition as a generic polyhedral complex in order to detect which region to check next. In contrast, our LayerCert framework considers the \emph{nested hyperplane arrangement} structure induced by the layers of the ReLU network and explores regions in a hierarchical manner. We show that, under certain conditions on the algorithm parameters, LayerCert provably reduces the number and size of the convex programs that one needs to solve compared to GeoCert. Furthermore, our LayerCert framework allows the incorporation of lower bounding routines based on convex relaxations to further improve performance. Experimental results demonstrate that LayerCert can significantly reduce both the number of convex programs solved and the running time over the state-of-the-art.

A Distributed Quasi-Newton Algorithm for Primal and Dual Regularized Empirical Risk Minimization

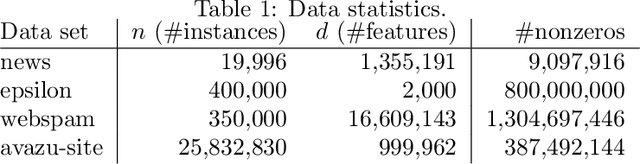
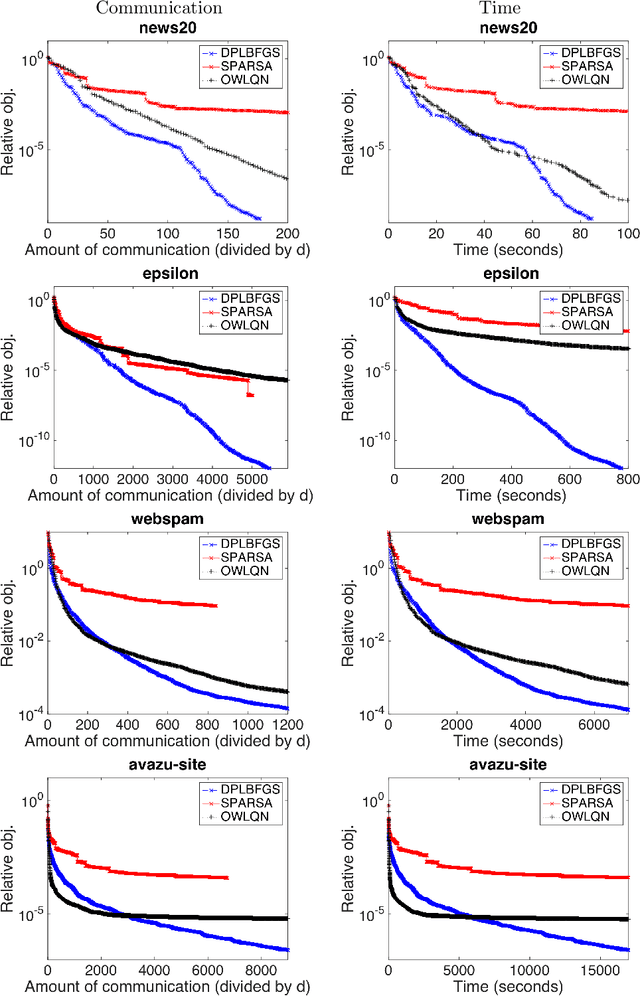
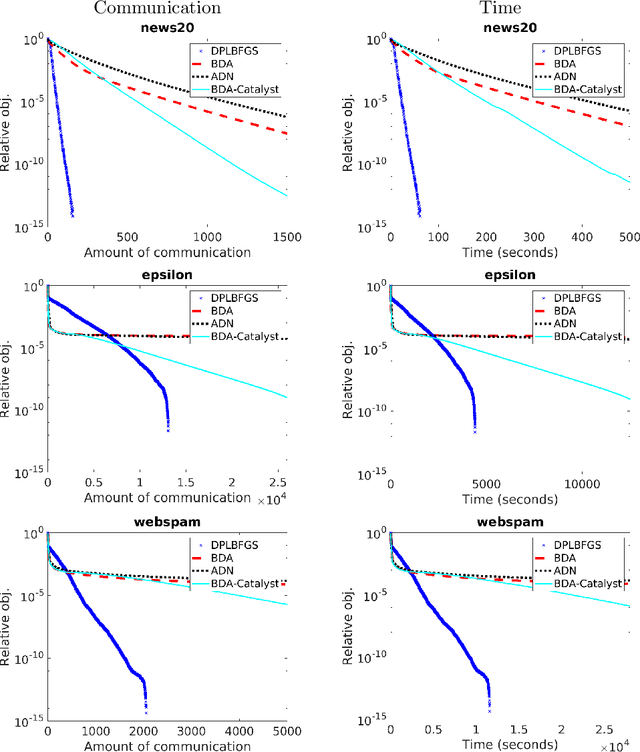
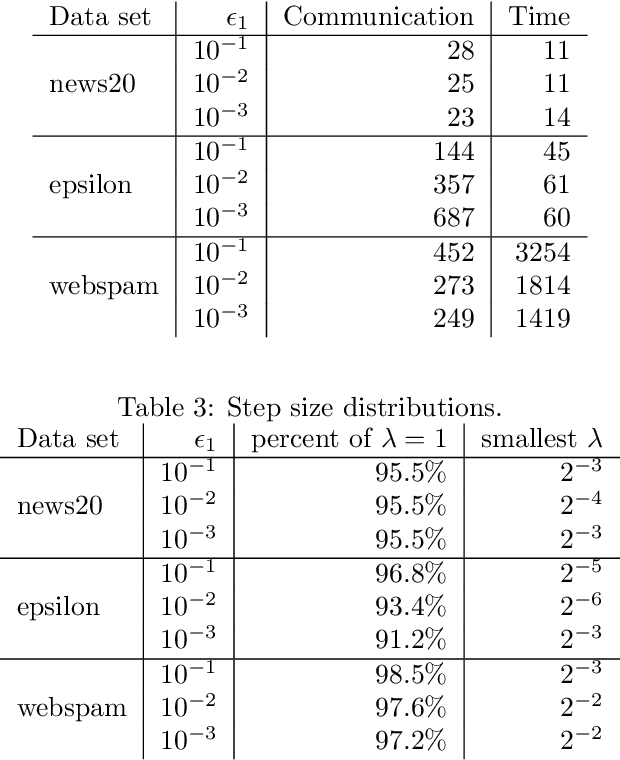
We propose a communication- and computation-efficient distributed optimization algorithm using second-order information for solving empirical risk minimization (ERM) problems with a nonsmooth regularization term. Our algorithm is applicable to both the primal and the dual ERM problem. Current second-order and quasi-Newton methods for this problem either do not work well in the distributed setting or work only for specific regularizers. Our algorithm uses successive quadratic approximations of the smooth part, and we describe how to maintain an approximation of the (generalized) Hessian and solve subproblems efficiently in a distributed manner. When applied to the distributed dual ERM problem, unlike state of the art that takes only the block-diagonal part of the Hessian, our approach is able to utilize global curvature information and is thus magnitudes faster. The proposed method enjoys global linear convergence for a broad range of non-strongly convex problems that includes the most commonly used ERMs, thus requiring lower communication complexity. It also converges on non-convex problems, so has the potential to be used on applications such as deep learning. Computational results demonstrate that our method significantly improves on communication cost and running time over the current state-of-the-art methods.

A Distributed Quasi-Newton Algorithm for Empirical Risk Minimization with Nonsmooth Regularization

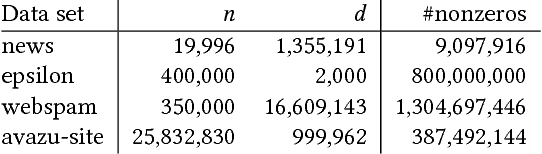
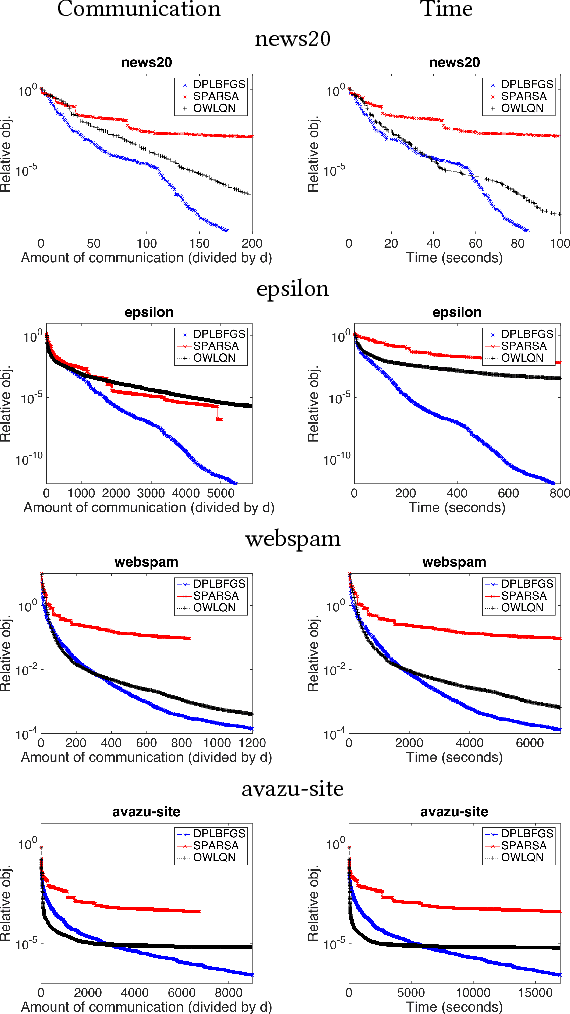
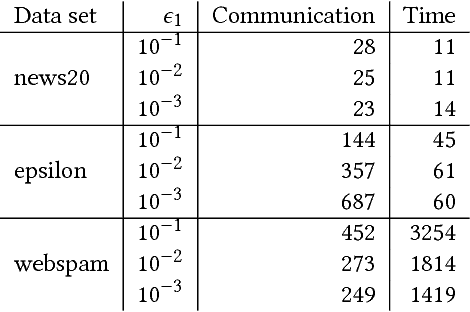
We propose a communication- and computation-efficient distributed optimization algorithm using second-order information for solving ERM problems with a nonsmooth regularization term. Current second-order and quasi-Newton methods for this problem either do not work well in the distributed setting or work only for specific regularizers. Our algorithm uses successive quadratic approximations, and we describe how to maintain an approximation of the Hessian and solve subproblems efficiently in a distributed manner. The proposed method enjoys global linear convergence for a broad range of non-strongly convex problems that includes the most commonly used ERMs, thus requiring lower communication complexity. It also converges on non-convex problems, so has the potential to be used on applications such as deep learning. Initial computational results on convex problems demonstrate that our method significantly improves on communication cost and running time over the current state-of-the-art methods.