A Distributed Quasi-Newton Algorithm for Empirical Risk Minimization with Nonsmooth Regularization
Paper and Code
May 26, 2018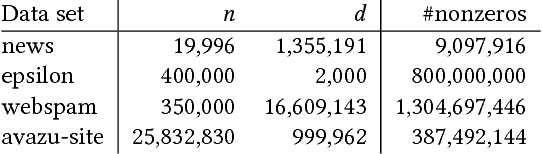
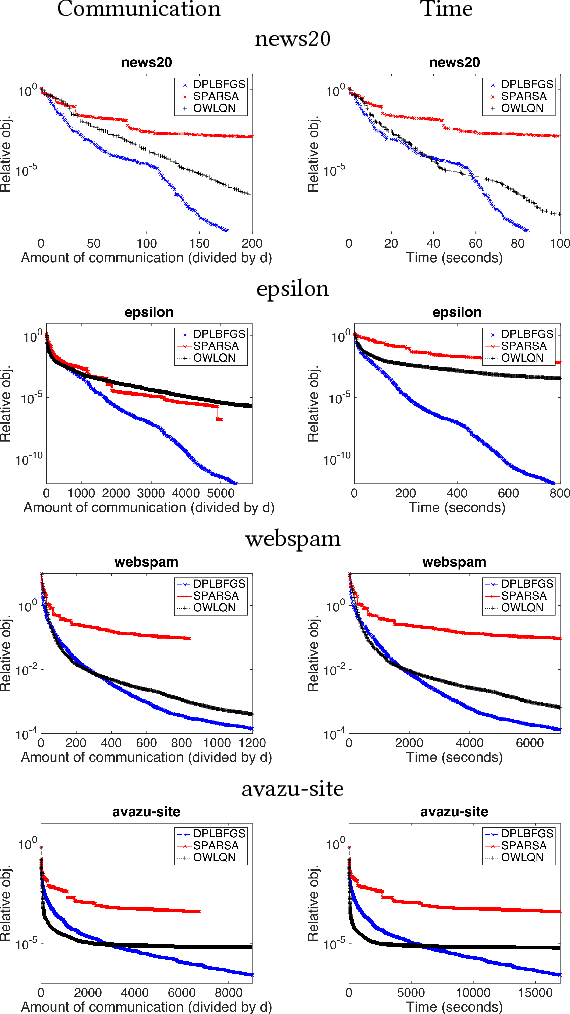
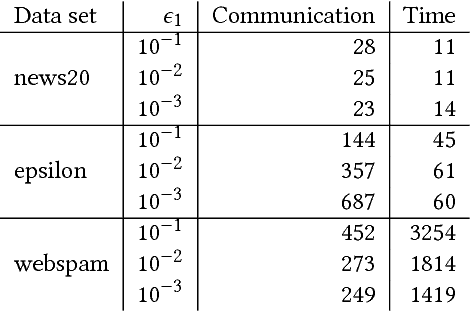

We propose a communication- and computation-efficient distributed optimization algorithm using second-order information for solving ERM problems with a nonsmooth regularization term. Current second-order and quasi-Newton methods for this problem either do not work well in the distributed setting or work only for specific regularizers. Our algorithm uses successive quadratic approximations, and we describe how to maintain an approximation of the Hessian and solve subproblems efficiently in a distributed manner. The proposed method enjoys global linear convergence for a broad range of non-strongly convex problems that includes the most commonly used ERMs, thus requiring lower communication complexity. It also converges on non-convex problems, so has the potential to be used on applications such as deep learning. Initial computational results on convex problems demonstrate that our method significantly improves on communication cost and running time over the current state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge