Hierarchical Verification for Adversarial Robustness
Paper and Code
Jul 23, 2020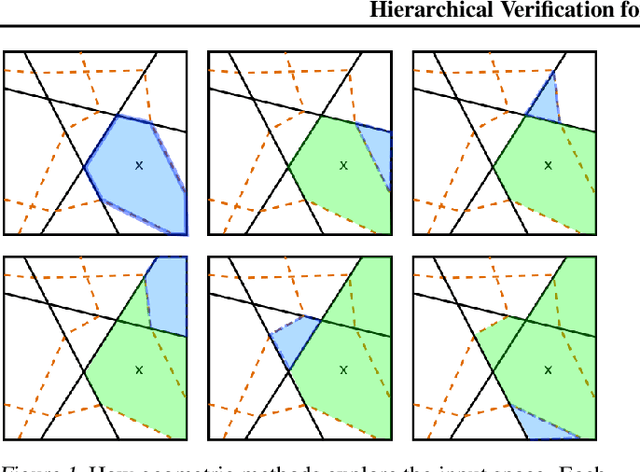
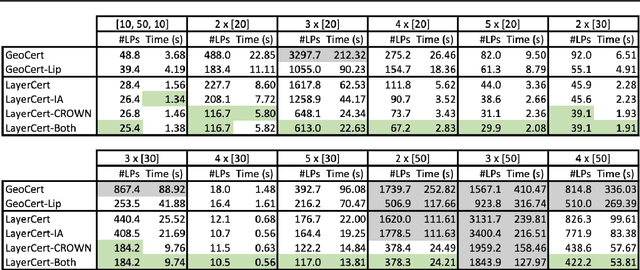
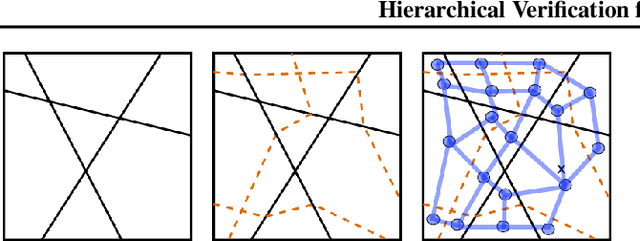
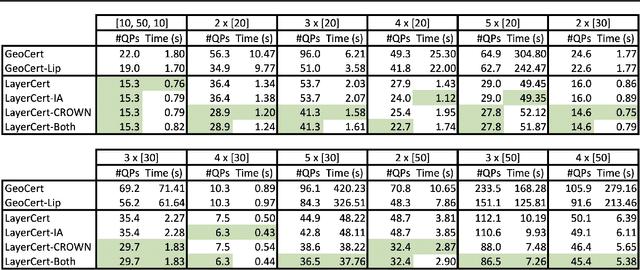
We introduce a new framework for the exact point-wise $\ell_p$ robustness verification problem that exploits the layer-wise geometric structure of deep feed-forward networks with rectified linear activations (ReLU networks). The activation regions of the network partition the input space, and one can verify the $\ell_p$ robustness around a point by checking all the activation regions within the desired radius. The GeoCert algorithm (Jordan et al., NeurIPS 2019) treats this partition as a generic polyhedral complex in order to detect which region to check next. In contrast, our LayerCert framework considers the \emph{nested hyperplane arrangement} structure induced by the layers of the ReLU network and explores regions in a hierarchical manner. We show that, under certain conditions on the algorithm parameters, LayerCert provably reduces the number and size of the convex programs that one needs to solve compared to GeoCert. Furthermore, our LayerCert framework allows the incorporation of lower bounding routines based on convex relaxations to further improve performance. Experimental results demonstrate that LayerCert can significantly reduce both the number of convex programs solved and the running time over the state-of-the-art.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge