GE2E-AC: Generalized End-to-End Loss Training for Accent Classification

Accent classification or AC is a task to predict the accent type of an input utterance, and it can be used as a preliminary step toward accented speech recognition and accent conversion. Existing studies have often achieved such classification by training a neural network model to minimize the classification error of the predicted accent label, which can be obtained as a model output. Since we optimize the entire model only from the perspective of classification loss during training time in this approach, the model might learn to predict the accent type from irrelevant features, such as individual speaker identity, which are not informative during test time. To address this problem, we propose a GE2E-AC, in which we train a model to extract accent embedding or AE of an input utterance such that the AEs of the same accent class get closer, instead of directly minimizing the classification loss. We experimentally show the effectiveness of the proposed GE2E-AC, compared to the baseline model trained with the conventional cross-entropy-based loss.

AutoLL: Automatic Linear Layout of Graphs based on Deep Neural Network

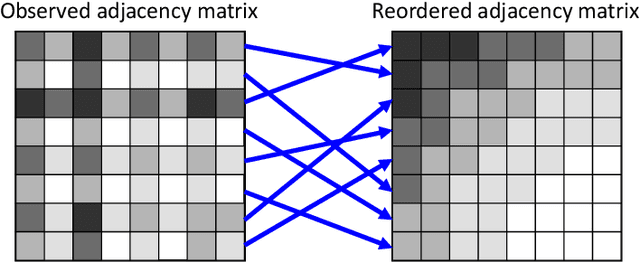
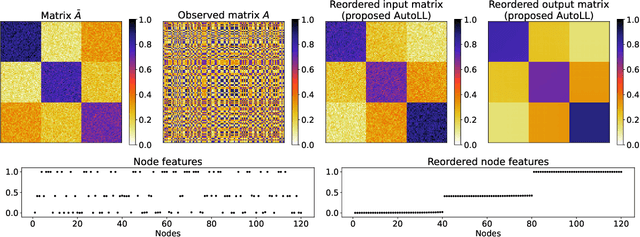
Linear layouts are a graph visualization method that can be used to capture an entry pattern in an adjacency matrix of a given graph. By reordering the node indices of the original adjacency matrix, linear layouts provide knowledge of latent graph structures. Conventional linear layout methods commonly aim to find an optimal reordering solution based on predefined features of a given matrix and loss function. However, prior knowledge of the appropriate features to use or structural patterns in a given adjacency matrix is not always available. In such a case, performing the reordering based on data-driven feature extraction without assuming a specific structure in an adjacency matrix is preferable. Recently, a neural-network-based matrix reordering method called DeepTMR has been proposed to perform this function. However, it is limited to a two-mode reordering (i.e., the rows and columns are reordered separately) and it cannot be applied in the one-mode setting (i.e., the same node order is used for reordering both rows and columns), owing to the characteristics of its model architecture. In this study, we extend DeepTMR and propose a new one-mode linear layout method referred to as AutoLL. We developed two types of neural network models, AutoLL-D and AutoLL-U, for reordering directed and undirected networks, respectively. To perform one-mode reordering, these AutoLL models have specific encoder architectures, which extract node features from an observed adjacency matrix. We conducted both qualitative and quantitative evaluations of the proposed approach, and the experimental results demonstrate its effectiveness.

Deep Two-Way Matrix Reordering for Relational Data Analysis

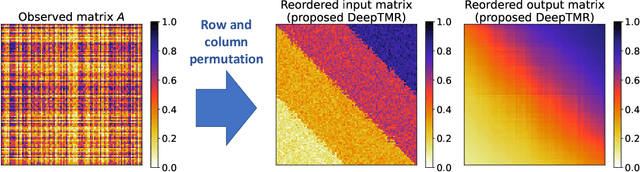
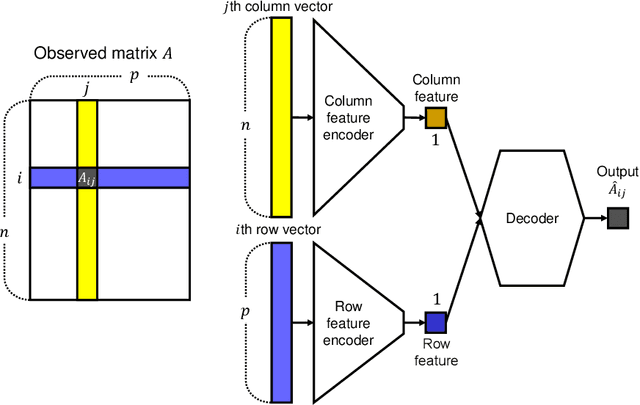
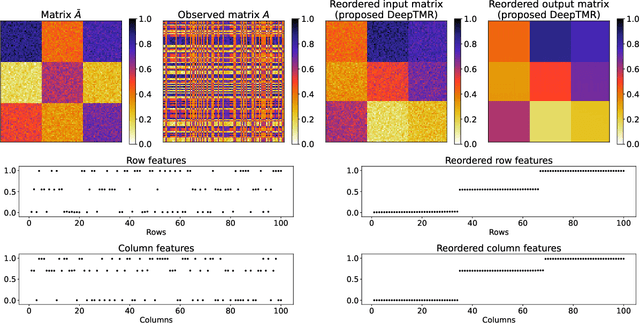
Matrix reordering is a task to permute the rows and columns of a given observed matrix such that the resulting reordered matrix shows meaningful or interpretable structural patterns. Most existing matrix reordering techniques share the common processes of extracting some feature representations from an observed matrix in a predefined manner, and applying matrix reordering based on it. However, in some practical cases, we do not always have prior knowledge about the structural pattern of an observed matrix. To address this problem, we propose a new matrix reordering method, called deep two-way matrix reordering (DeepTMR), using a neural network model. The trained network can automatically extract nonlinear row/column features from an observed matrix, which can then be used for matrix reordering. Moreover, the proposed DeepTMR provides the denoised mean matrix of a given observed matrix as an output of the trained network. This denoised mean matrix can be used to visualize the global structure of the reordered observed matrix. We demonstrate the effectiveness of the proposed DeepTMR by applying it to both synthetic and practical datasets.

Goodness-of-fit Test on the Number of Biclusters in Relational Data Matrix

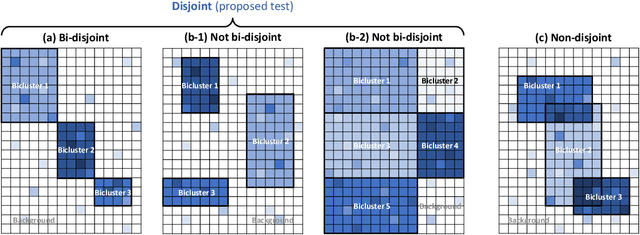
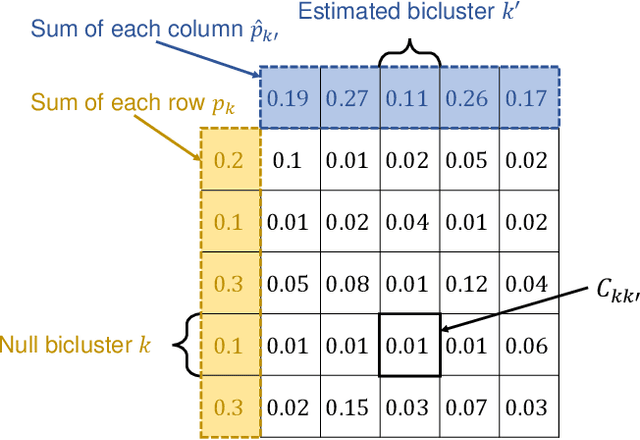
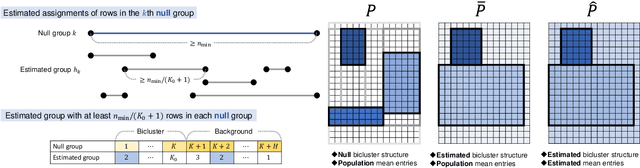
Biclustering is a problem to detect homogeneous submatrices in a given observed matrix, and it has been shown to be an effective tool for relational data analysis. Although there have been many studies for estimating the underlying bicluster structure of a matrix, few have enabled us to determine the appropriate number of biclusters in an observed matrix. Recently, a statistical test on the number of biclusters has been proposed for a regular-grid bicluster structure, where we assume that the latent bicluster structure can be represented by row-column clustering. However, when the latent bicluster structure does not satisfy such regular-grid assumption, the previous test requires too many biclusters (i.e., finer bicluster structure) for the null hypothesis to be accepted, which is not desirable in terms of interpreting the accepted bicluster structure. In this paper, we propose a new statistical test on the number of biclusters that does not require the regular-grid assumption, and derive the asymptotic behavior of the proposed test statistic in both null and alternative cases. To develop the proposed test, we construct a consistent submatrix localization algorithm, that is, the probability that it outputs the correct bicluster structure converges to one. We show the effectiveness of the proposed method by applying it to both synthetic and practical relational data matrices.

X-DC: Explainable Deep Clustering based on Learnable Spectrogram Templates

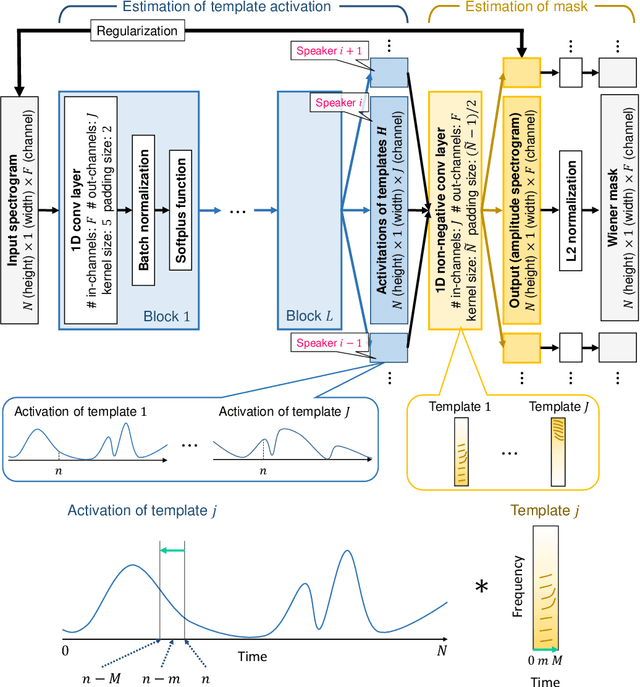
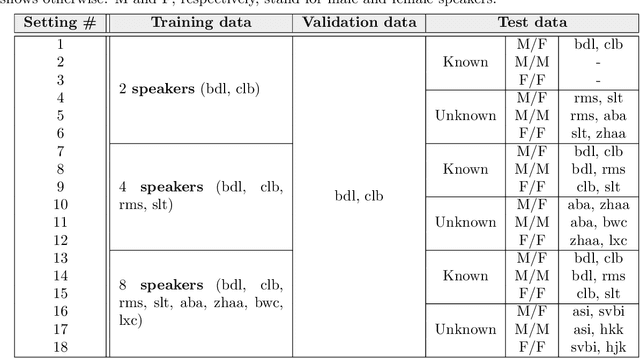
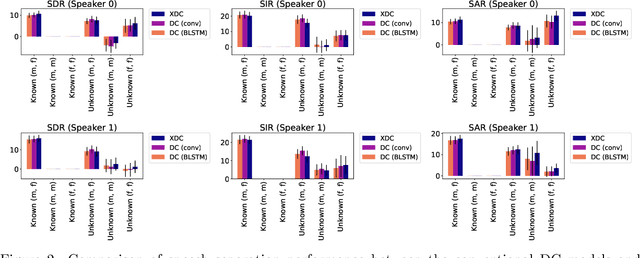
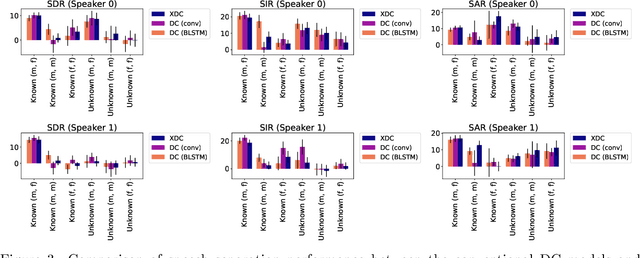
Deep neural networks (DNNs) have achieved substantial predictive performance in various speech processing tasks. Particularly, it has been shown that a monaural speech separation task can be successfully solved with a DNN-based method called deep clustering (DC), which uses a DNN to describe the process of assigning a continuous vector to each time-frequency (TF) bin and measure how likely each pair of TF bins is to be dominated by the same speaker. In DC, the DNN is trained so that the embedding vectors for the TF bins dominated by the same speaker are forced to get close to each other. One concern regarding DC is that the embedding process described by a DNN has a black-box structure, which is usually very hard to interpret. The potential weakness owing to the non-interpretable black-box structure is that it lacks the flexibility of addressing the mismatch between training and test conditions (caused by reverberation, for instance). To overcome this limitation, in this paper, we propose the concept of explainable deep clustering (X-DC), whose network architecture can be interpreted as a process of fitting learnable spectrogram templates to an input spectrogram followed by Wiener filtering. During training, the elements of the spectrogram templates and their activations are constrained to be non-negative, which facilitates the sparsity of their values and thus improves interpretability. The main advantage of this framework is that it naturally allows us to incorporate a model adaptation mechanism into the network thanks to its physically interpretable structure. We experimentally show that the proposed X-DC enables us to visualize and understand the clues for the model to determine the embedding vectors while achieving speech separation performance comparable to that of the original DC models.

Selective Inference for Latent Block Models

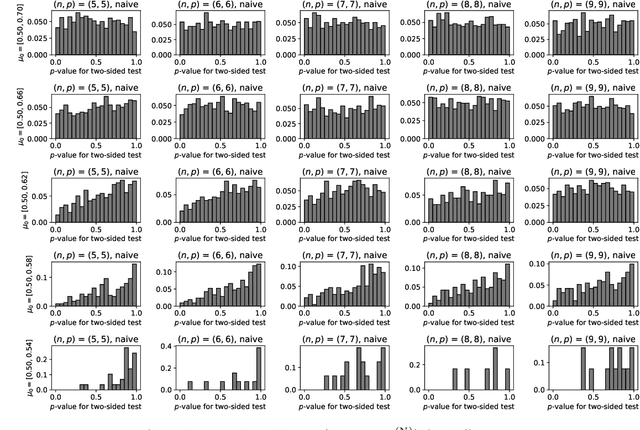
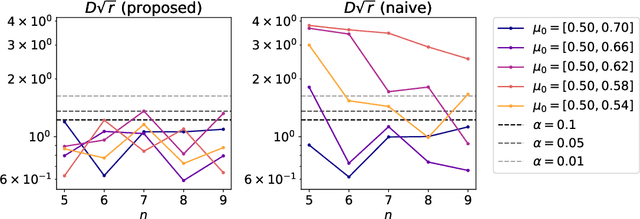
Model selection in latent block models has been a challenging but important task in the field of statistics. Specifically, a major challenge is encountered when constructing a test on a block structure obtained by applying a specific clustering algorithm to a finite size matrix. In this case, it becomes crucial to consider the selective bias in the block structure, that is, the block structure is selected from all the possible cluster memberships based on some criterion by the clustering algorithm. To cope with this problem, this study provides a selective inference method for latent block models. Specifically, we construct a statistical test on a set of row and column cluster memberships of a latent block model, which is given by a squared residue minimization algorithm. The proposed test, by its nature, includes and thus can also be used as the test on the set of row and column cluster numbers. We also propose an approximated version of the test based on simulated annealing to avoid combinatorial explosion in searching the optimal block structure. The results show that the proposed exact and approximated tests work effectively, compared to the naive test that did not take the selective bias into account.

Goodness-of-fit Test for Latent Block Models

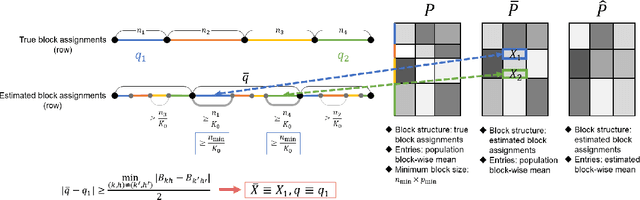
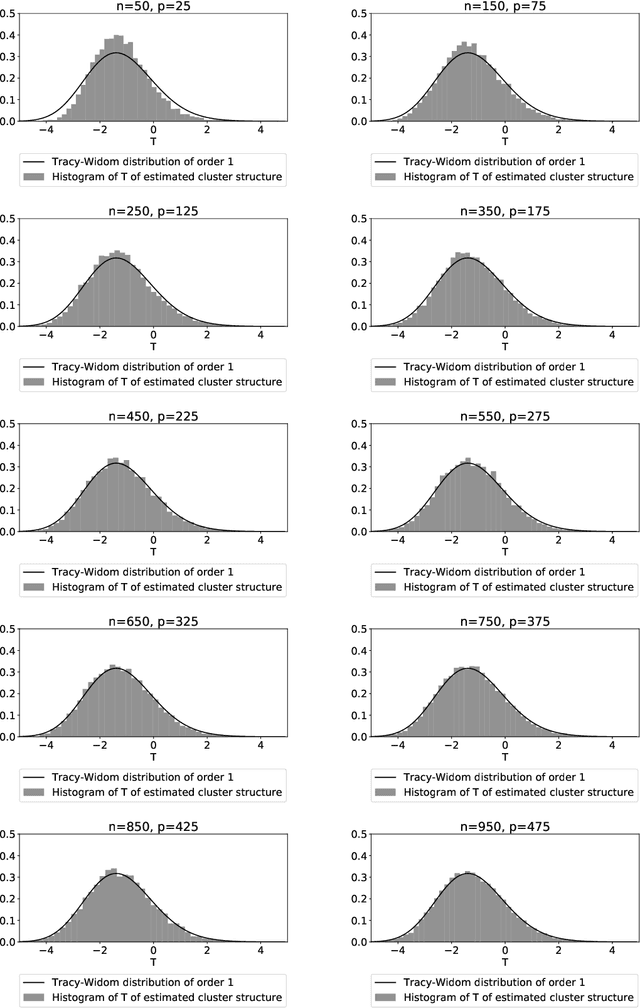
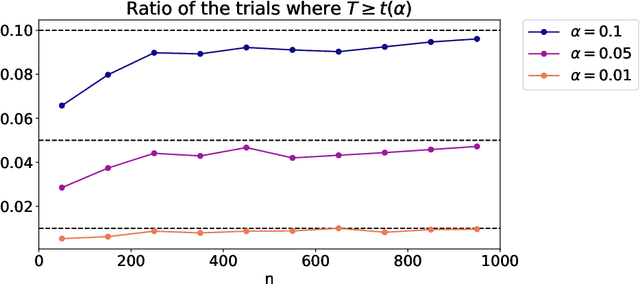
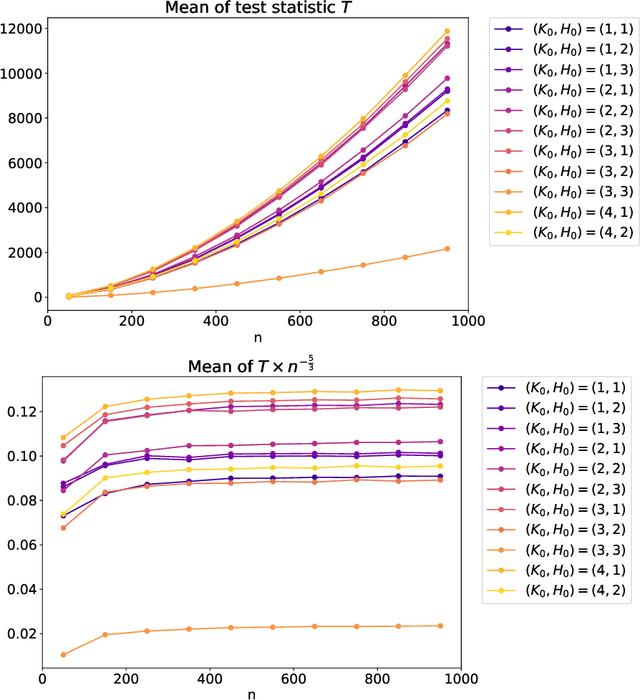
Latent block models are used for probabilistic biclustering, which is shown to be an effective method for analyzing various relational data sets. However, there has been no statistical test method for determining the row and column cluster numbers of latent block models. Recent studies have constructed statistical-test-based methods for stochastic block models, which assume that the observed matrix is a square symmetric matrix and that the cluster assignments are the same for rows and columns. In this study, we developed a new goodness-of-fit test for latent block models to test whether an observed data matrix fits a given set of row and column cluster numbers, or it consists of more clusters in at least one direction of the row and the column. To construct the test method, we used a result from the random matrix theory for a sample covariance matrix. We experimentally demonstrated the effectiveness of the proposed method by showing the asymptotic behavior of the test statistic and measuring the test accuracy.

Interpreting Layered Neural Networks via Hierarchical Modular Representation

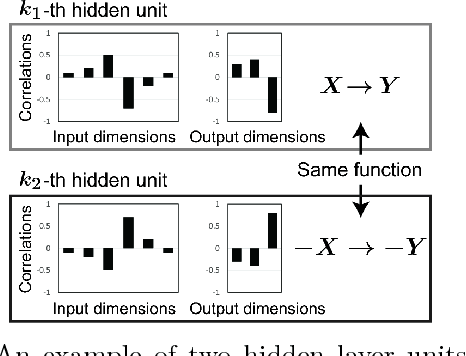
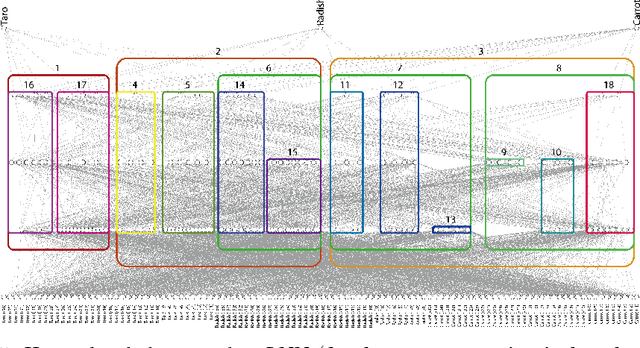
Interpreting the prediction mechanism of complex models is currently one of the most important tasks in the machine learning field, especially with layered neural networks, which have achieved high predictive performance with various practical data sets. To reveal the global structure of a trained neural network in an interpretable way, a series of clustering methods have been proposed, which decompose the units into clusters according to the similarity of their inference roles. The main problems in these studies were that (1) we have no prior knowledge about the optimal resolution for the decomposition, or the appropriate number of clusters, and (2) there was no method with which to acquire knowledge about whether the outputs of each cluster have a positive or negative correlation with the input and output dimension values. In this paper, to solve these problems, we propose a method for obtaining a hierarchical modular representation of a layered neural network. The application of a hierarchical clustering method to a trained network reveals a tree-structured relationship among hidden layer units, based on their feature vectors defined by their correlation with the input and output dimension values.

Knowledge Discovery from Layered Neural Networks based on Non-negative Task Decomposition

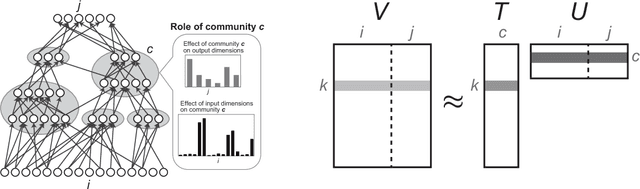
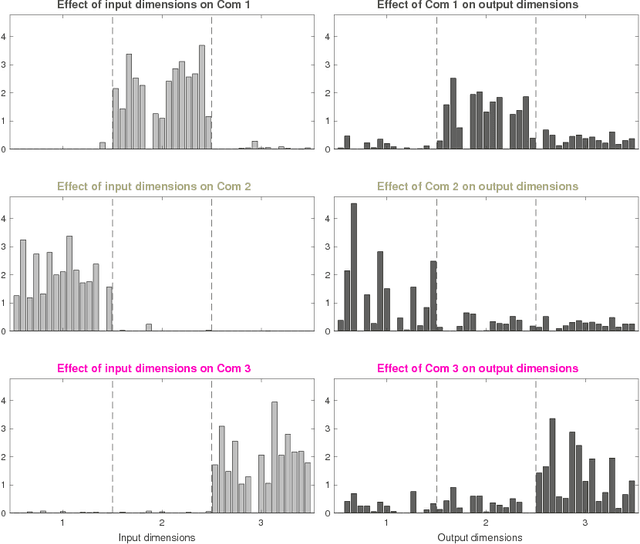
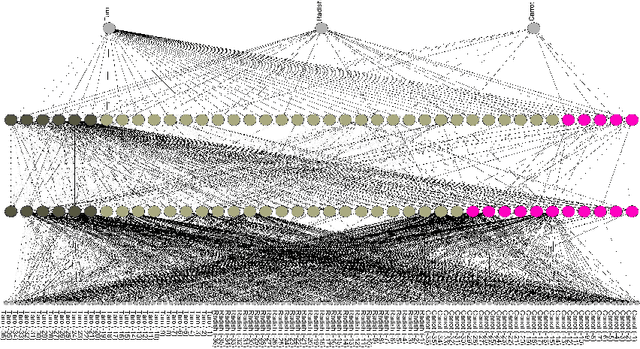
Interpretability has become an important issue in the machine learning field, along with the success of layered neural networks in various practical tasks. Since a trained layered neural network consists of a complex nonlinear relationship between large number of parameters, we failed to understand how they could achieve input-output mappings with a given data set. In this paper, we propose the non-negative task decomposition method, which applies non-negative matrix factorization to a trained layered neural network. This enables us to decompose the inference mechanism of a trained layered neural network into multiple principal tasks of input-output mapping, and reveal the roles of hidden units in terms of their contribution to each principal task.

Understanding Community Structure in Layered Neural Networks

A layered neural network is now one of the most common choices for the prediction of high-dimensional practical data sets, where the relationship between input and output data is complex and cannot be represented well by simple conventional models. Its effectiveness is shown in various tasks, however, the lack of interpretability of the trained result by a layered neural network has limited its application area. In our previous studies, we proposed methods for extracting a simplified global structure of a trained layered neural network by classifying the units into communities according to their connection patterns with adjacent layers. These methods provided us with knowledge about the strength of the relationship between communities from the existence of bundled connections, which are determined by threshold processing of the connection ratio between pairs of communities. However, it has been difficult to understand the role of each community quantitatively by observing the modular structure. We could only know to which sets of the input and output dimensions each community was mainly connected, by tracing the bundled connections from the community to the input and output layers. Another problem is that the finally obtained modular structure is changed greatly depending on the setting of the threshold hyperparameter used for determining bundled connections. In this paper, we propose a new method for interpreting quantitatively the role of each community in inference, by defining the effect of each input dimension on a community, and the effect of a community on each output dimension. We show experimentally that our proposed method can reveal the role of each part of a layered neural network by applying the neural networks to three types of data sets, extracting communities from the trained network, and applying the proposed method to the community structure.