Goodness-of-fit Test on the Number of Biclusters in Relational Data Matrix

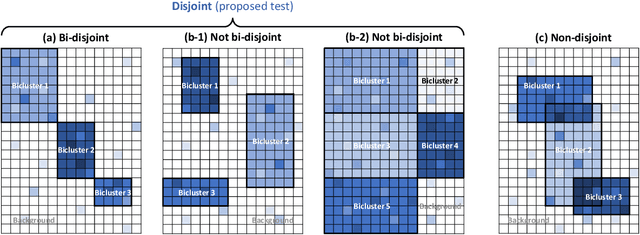
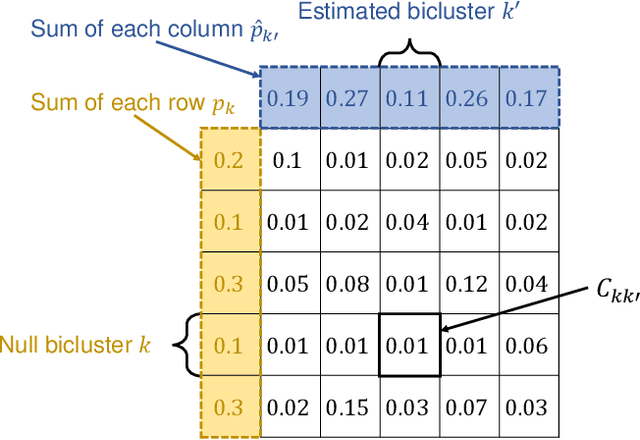
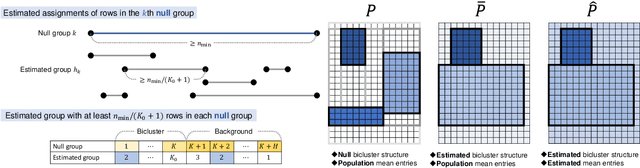
Biclustering is a problem to detect homogeneous submatrices in a given observed matrix, and it has been shown to be an effective tool for relational data analysis. Although there have been many studies for estimating the underlying bicluster structure of a matrix, few have enabled us to determine the appropriate number of biclusters in an observed matrix. Recently, a statistical test on the number of biclusters has been proposed for a regular-grid bicluster structure, where we assume that the latent bicluster structure can be represented by row-column clustering. However, when the latent bicluster structure does not satisfy such regular-grid assumption, the previous test requires too many biclusters (i.e., finer bicluster structure) for the null hypothesis to be accepted, which is not desirable in terms of interpreting the accepted bicluster structure. In this paper, we propose a new statistical test on the number of biclusters that does not require the regular-grid assumption, and derive the asymptotic behavior of the proposed test statistic in both null and alternative cases. To develop the proposed test, we construct a consistent submatrix localization algorithm, that is, the probability that it outputs the correct bicluster structure converges to one. We show the effectiveness of the proposed method by applying it to both synthetic and practical relational data matrices.