Generative Adversarial Image Synthesis with Decision Tree Latent Controller

This paper proposes the decision tree latent controller generative adversarial network (DTLC-GAN), an extension of a GAN that can learn hierarchically interpretable representations without relying on detailed supervision. To impose a hierarchical inclusion structure on latent variables, we incorporate a new architecture called the DTLC into the generator input. The DTLC has a multiple-layer tree structure in which the ON or OFF of the child node codes is controlled by the parent node codes. By using this architecture hierarchically, we can obtain the latent space in which the lower layer codes are selectively used depending on the higher layer ones. To make the latent codes capture salient semantic features of images in a hierarchically disentangled manner in the DTLC, we also propose a hierarchical conditional mutual information regularization and optimize it with a newly defined curriculum learning method that we propose as well. This makes it possible to discover hierarchically interpretable representations in a layer-by-layer manner on the basis of information gain by only using a single DTLC-GAN model. We evaluated the DTLC-GAN on various datasets, i.e., MNIST, CIFAR-10, Tiny ImageNet, 3D Faces, and CelebA, and confirmed that the DTLC-GAN can learn hierarchically interpretable representations with either unsupervised or weakly supervised settings. Furthermore, we applied the DTLC-GAN to image-retrieval tasks and showed its effectiveness in representation learning.

Knowledge Discovery from Layered Neural Networks based on Non-negative Task Decomposition

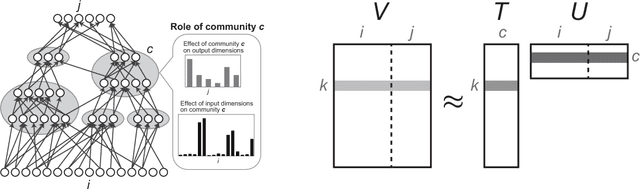
Interpretability has become an important issue in the machine learning field, along with the success of layered neural networks in various practical tasks. Since a trained layered neural network consists of a complex nonlinear relationship between large number of parameters, we failed to understand how they could achieve input-output mappings with a given data set. In this paper, we propose the non-negative task decomposition method, which applies non-negative matrix factorization to a trained layered neural network. This enables us to decompose the inference mechanism of a trained layered neural network into multiple principal tasks of input-output mapping, and reveal the roles of hidden units in terms of their contribution to each principal task.

Understanding Community Structure in Layered Neural Networks

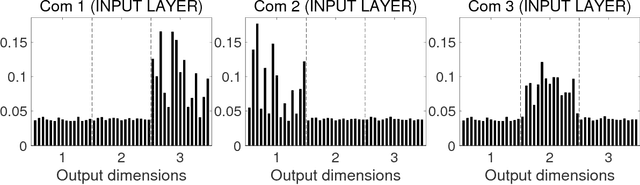
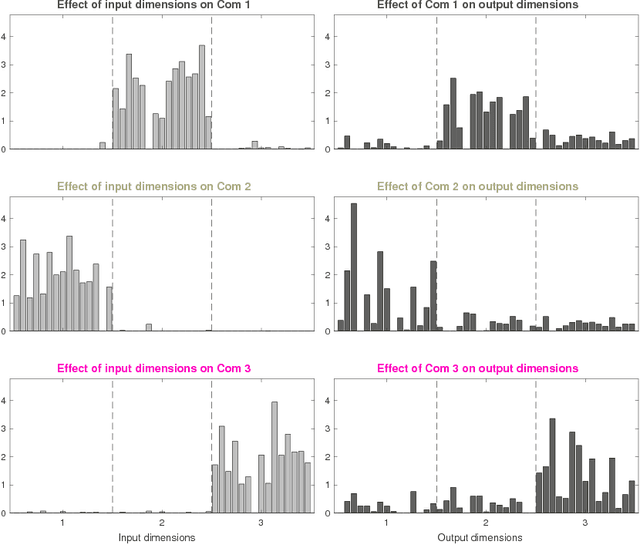
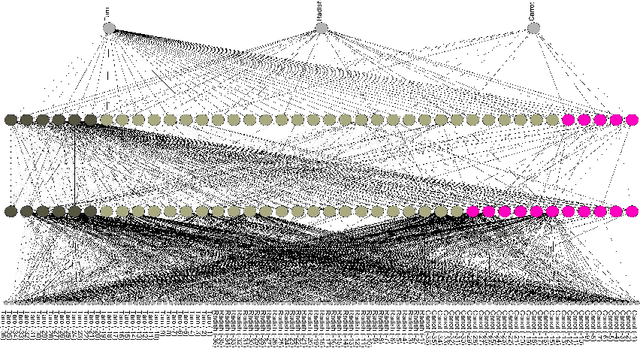
A layered neural network is now one of the most common choices for the prediction of high-dimensional practical data sets, where the relationship between input and output data is complex and cannot be represented well by simple conventional models. Its effectiveness is shown in various tasks, however, the lack of interpretability of the trained result by a layered neural network has limited its application area. In our previous studies, we proposed methods for extracting a simplified global structure of a trained layered neural network by classifying the units into communities according to their connection patterns with adjacent layers. These methods provided us with knowledge about the strength of the relationship between communities from the existence of bundled connections, which are determined by threshold processing of the connection ratio between pairs of communities. However, it has been difficult to understand the role of each community quantitatively by observing the modular structure. We could only know to which sets of the input and output dimensions each community was mainly connected, by tracing the bundled connections from the community to the input and output layers. Another problem is that the finally obtained modular structure is changed greatly depending on the setting of the threshold hyperparameter used for determining bundled connections. In this paper, we propose a new method for interpreting quantitatively the role of each community in inference, by defining the effect of each input dimension on a community, and the effect of a community on each output dimension. We show experimentally that our proposed method can reveal the role of each part of a layered neural network by applying the neural networks to three types of data sets, extracting communities from the trained network, and applying the proposed method to the community structure.

Modular Representation of Layered Neural Networks

Layered neural networks have greatly improved the performance of various applications including image processing, speech recognition, natural language processing, and bioinformatics. However, it is still difficult to discover or interpret knowledge from the inference provided by a layered neural network, since its internal representation has many nonlinear and complex parameters embedded in hierarchical layers. Therefore, it becomes important to establish a new methodology by which layered neural networks can be understood. In this paper, we propose a new method for extracting a global and simplified structure from a layered neural network. Based on network analysis, the proposed method detects communities or clusters of units with similar connection patterns. We show its effectiveness by applying it to three use cases. (1) Network decomposition: it can decompose a trained neural network into multiple small independent networks thus dividing the problem and reducing the computation time. (2) Training assessment: the appropriateness of a trained result with a given hyperparameter or randomly chosen initial parameters can be evaluated by using a modularity index. And (3) data analysis: in practical data it reveals the community structure in the input, hidden, and output layers, which serves as a clue for discovering knowledge from a trained neural network.