Understanding Community Structure in Layered Neural Networks

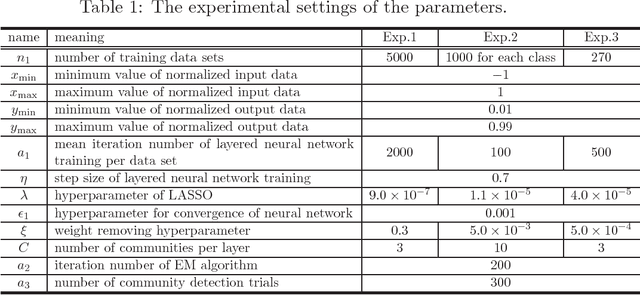
A layered neural network is now one of the most common choices for the prediction of high-dimensional practical data sets, where the relationship between input and output data is complex and cannot be represented well by simple conventional models. Its effectiveness is shown in various tasks, however, the lack of interpretability of the trained result by a layered neural network has limited its application area. In our previous studies, we proposed methods for extracting a simplified global structure of a trained layered neural network by classifying the units into communities according to their connection patterns with adjacent layers. These methods provided us with knowledge about the strength of the relationship between communities from the existence of bundled connections, which are determined by threshold processing of the connection ratio between pairs of communities. However, it has been difficult to understand the role of each community quantitatively by observing the modular structure. We could only know to which sets of the input and output dimensions each community was mainly connected, by tracing the bundled connections from the community to the input and output layers. Another problem is that the finally obtained modular structure is changed greatly depending on the setting of the threshold hyperparameter used for determining bundled connections. In this paper, we propose a new method for interpreting quantitatively the role of each community in inference, by defining the effect of each input dimension on a community, and the effect of a community on each output dimension. We show experimentally that our proposed method can reveal the role of each part of a layered neural network by applying the neural networks to three types of data sets, extracting communities from the trained network, and applying the proposed method to the community structure.