Benchmarking Continuous Dynamic Multi-Objective Optimization: Survey and Generalized Test Suite

Dynamic multi-objective optimization (DMOO) has recently attracted increasing interest from both academic researchers and engineering practitioners, as numerous real-world applications that evolve over time can be naturally formulated as dynamic multi-objective optimization problems (DMOPs). This growing trend necessitates advanced benchmarks for the rigorous evaluation of optimization algorithms under realistic conditions. This paper introduces a comprehensive and principled framework for constructing highly realistic and challenging DMOO benchmarks. The proposed framework features several novel components: a generalized formulation that allows the Pareto-optimal Set (PS) to change on hypersurfaces, a mechanism for creating controlled variable contribution imbalances to generate heterogeneous landscapes, and dynamic rotation matrices for inducing time-varying variable interactions and non-separability. Furthermore, we incorporate a temporal perturbation mechanism to simulate irregular environmental changes and propose a generalized time-linkage mechanism that systematically embeds historical solution quality into future problems, thereby capturing critical real-world phenomena such as error accumulation and time-deception. Extensive experimental results validate the effectiveness of the proposed framework, demonstrating its superiority over conventional benchmarks in terms of realism, complexity, and its capability for discriminating state-of-the-art algorithmic performance. This work establishes a new standard for dynamic multi-objective optimization benchmarking, providing a powerful tool for the development and evaluation of next-generation algorithms capable of addressing the complexities of real-world dynamic systems.

Distributed Evolution Strategies with Multi-Level Learning for Large-Scale Black-Box Optimization

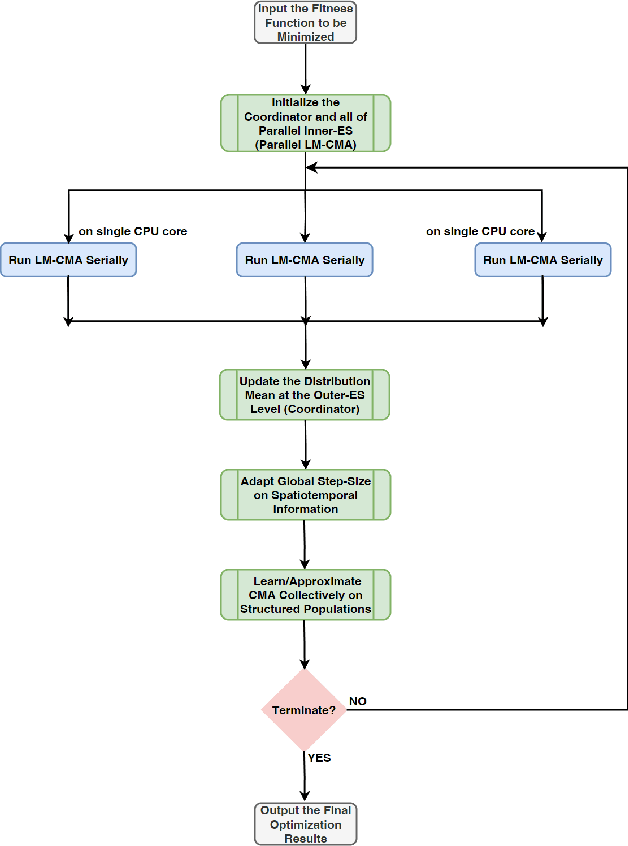
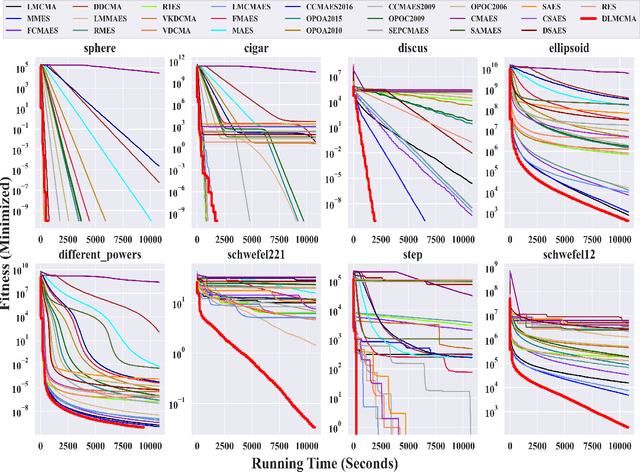
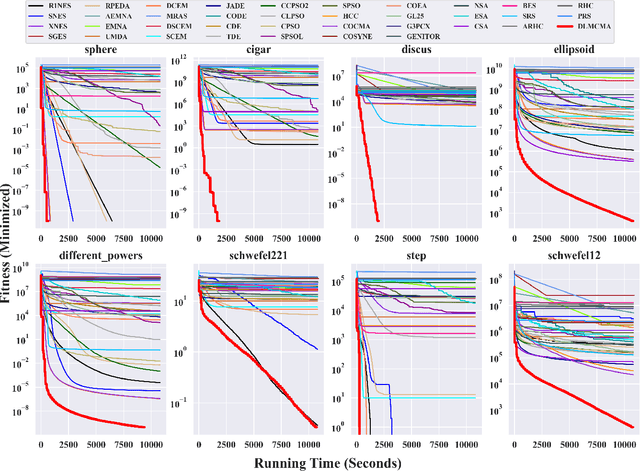
In the post-Moore era, the main performance gains of black-box optimizers are increasingly depending upon parallelism, especially for large-scale optimization (LSO). In this paper, we propose to parallelize the well-established covariance matrix adaptation evolution strategy (CMA-ES) and in particular its one latest variant called limited-memory CMA (LM-CMA) for LSO. To achieve scalability while maintaining the invariance property as much as possible, we present a multilevel learning-based meta-framework. Owing to its hierarchically organized structure, Meta-ES is well-suited to implement our distributed meta-framework, wherein the outer-ES controls strategy parameters while all parallel inner-ESs run the serial LM-CMA with different settings. For the distribution mean update of the outer-ES, both the elitist and multi-recombination strategy are used in parallel to avoid stagnation and regression, respectively. To exploit spatiotemporal information, the global step-size adaptation combines Meta-ES with the parallel cumulative step-size adaptation. After each isolation time, our meta-framework employs both the structure and parameter learning strategy to combine aligned evolution paths for CMA reconstruction. Experiments on a set of large-scale benchmarking functions with memory-intensive evaluations, arguably reflecting many data-driven optimization problems, validate the benefits (e.g., scalability w.r.t. CPU cores, effectiveness w.r.t. solution quality, and adaptability w.r.t. second-order learning) and costs of our meta-framework.

Cooperative Coevolution for Non-Separable Large-Scale Black-Box Optimization: Convergence Analyses and Distributed Accelerations

Given the ubiquity of non-separable optimization problems in real worlds, in this paper we analyze and extend the large-scale version of the well-known cooperative coevolution (CC), a divide-and-conquer optimization framework, on non-separable functions. First, we reveal empirical reasons of why decomposition-based methods are preferred or not in practice on some non-separable large-scale problems, which have not been clearly pointed out in many previous CC papers. Then, we formalize CC to a continuous game model via simplification, but without losing its essential property. Different from previous evolutionary game theory for CC, our new model provides a much simpler but useful viewpoint to analyze its convergence, since only the pure Nash equilibrium concept is needed and more general fitness landscapes can be explicitly considered. Based on convergence analyses, we propose a hierarchical decomposition strategy for better generalization, as for any decomposition there is a risk of getting trapped into a suboptimal Nash equilibrium. Finally, we use powerful distributed computing to accelerate it under the multi-level learning framework, which combines the fine-tuning ability from decomposition with the invariance property of CMA-ES. Experiments on a set of high-dimensional functions validate both its search performance and scalability (w.r.t. CPU cores) on a clustering computing platform with 400 CPU cores.

PyPop7: A Pure-Python Library for Population-Based Black-Box Optimization

In this paper, we present a pure-Python open-source library, called PyPop7, for black-box optimization (BBO). It provides a unified and modular interface for more than 60 versions and variants of different black-box optimization algorithms, particularly population-based optimizers, which can be classified into 12 popular families: Evolution Strategies (ES), Natural Evolution Strategies (NES), Estimation of Distribution Algorithms (EDA), Cross-Entropy Method (CEM), Differential Evolution (DE), Particle Swarm Optimizer (PSO), Cooperative Coevolution (CC), Simulated Annealing (SA), Genetic Algorithms (GA), Evolutionary Programming (EP), Pattern Search (PS), and Random Search (RS). It also provides many examples, interesting tutorials, and full-fledged API documentations. Through this new library, we expect to provide a well-designed platform for benchmarking of optimizers and promote their real-world applications, especially for large-scale BBO. Its source code and documentations are available at https://github.com/Evolutionary-Intelligence/pypop and https://pypop.readthedocs.io/en/latest, respectively.