SEEK: Self-adaptive Explainable Kernel For Nonstationary Gaussian Processes

Gaussian processes (GPs) are powerful probabilistic models that define flexible priors over functions, offering strong interpretability and uncertainty quantification. However, GP models often rely on simple, stationary kernels which can lead to suboptimal predictions and miscalibrated uncertainty estimates, especially in nonstationary real-world applications. In this paper, we introduce SEEK, a novel class of learnable kernels to model complex, nonstationary functions via GPs. Inspired by artificial neurons, SEEK is derived from first principles to ensure symmetry and positive semi-definiteness, key properties of valid kernels. The proposed method achieves flexible and adaptive nonstationarity by learning a mapping from a set of base kernels. Compared to existing techniques, our approach is more interpretable and much less prone to overfitting. We conduct comprehensive sensitivity analyses and comparative studies to demonstrate that our approach is not robust to only many of its design choices, but also outperforms existing stationary/nonstationary kernels in both mean prediction accuracy and uncertainty quantification.

Operator Learning with Gaussian Processes

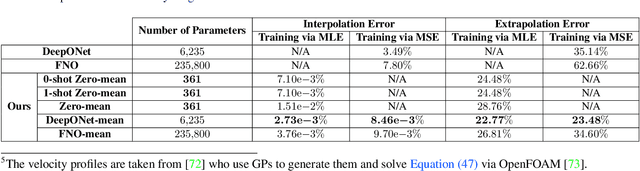
Operator learning focuses on approximating mappings $\mathcal{G}^\dagger:\mathcal{U} \rightarrow\mathcal{V}$ between infinite-dimensional spaces of functions, such as $u: \Omega_u\rightarrow\mathbb{R}$ and $v: \Omega_v\rightarrow\mathbb{R}$. This makes it particularly suitable for solving parametric nonlinear partial differential equations (PDEs). While most machine learning methods for operator learning rely on variants of deep neural networks (NNs), recent studies have shown that Gaussian Processes (GPs) are also competitive while offering interpretability and theoretical guarantees. In this paper, we introduce a hybrid GP/NN-based framework for operator learning that leverages the strengths of both methods. Instead of approximating the function-valued operator $\mathcal{G}^\dagger$, we use a GP to approximate its associated real-valued bilinear form $\widetilde{\mathcal{G}}^\dagger: \mathcal{U}\times\mathcal{V}^*\rightarrow\mathbb{R}.$ This bilinear form is defined by $\widetilde{\mathcal{G}}^\dagger(u,\varphi) := [\varphi,\mathcal{G}^\dagger(u)],$ which allows us to recover the operator $\mathcal{G}^\dagger$ through $\mathcal{G}^\dagger(u)(y)=\widetilde{\mathcal{G}}^\dagger(u,\delta_y).$ The GP mean function can be zero or parameterized by a neural operator and for each setting we develop a robust training mechanism based on maximum likelihood estimation (MLE) that can optionally leverage the physics involved. Numerical benchmarks show that (1) it improves the performance of a base neural operator by using it as the mean function of a GP, and (2) it enables zero-shot data-driven models for accurate predictions without prior training. Our framework also handles multi-output operators where $\mathcal{G}^\dagger:\mathcal{U} \rightarrow\prod_{s=1}^S\mathcal{V}^s$, and benefits from computational speed-ups via product kernel structures and Kronecker product matrix representations.

Simultaneous and Meshfree Topology Optimization with Physics-informed Gaussian Processes

Topology optimization (TO) provides a principled mathematical approach for optimizing the performance of a structure by designing its material spatial distribution in a pre-defined domain and subject to a set of constraints. The majority of existing TO approaches leverage numerical solvers for design evaluations during the optimization and hence have a nested nature and rely on discretizing the design variables. Contrary to these approaches, herein we develop a new class of TO methods based on the framework of Gaussian processes (GPs) whose mean functions are parameterized via deep neural networks. Specifically, we place GP priors on all design and state variables to represent them via parameterized continuous functions. These GPs share a deep neural network as their mean function but have as many independent kernels as there are state and design variables. We estimate all the parameters of our model in a single for loop that optimizes a penalized version of the performance metric where the penalty terms correspond to the state equations and design constraints. Attractive features of our approach include $(1)$ having a built-in continuation nature since the performance metric is optimized at the same time that the state equations are solved, and $(2)$ being discretization-invariant and accommodating complex domains and topologies. To test our method against conventional TO approaches implemented in commercial software, we evaluate it on four problems involving the minimization of dissipated power in Stokes flow. The results indicate that our approach does not need filtering techniques, has consistent computational costs, and is highly robust against random initializations and problem setup.

Neural Networks with Kernel-Weighted Corrective Residuals for Solving Partial Differential Equations

Physics-informed machine learning (PIML) has emerged as a promising alternative to conventional numerical methods for solving partial differential equations (PDEs). PIML models are increasingly built via deep neural networks (NNs) whose architecture and training process are designed such that the network satisfies the PDE system. While such PIML models have substantially advanced over the past few years, their performance is still very sensitive to the NN's architecture and loss function. Motivated by this limitation, we introduce kernel-weighted Corrective Residuals (CoRes) to integrate the strengths of kernel methods and deep NNs for solving nonlinear PDE systems. To achieve this integration, we design a modular and robust framework which consistently outperforms competing methods in solving a broad range of benchmark problems. This performance improvement has a theoretical justification and is particularly attractive since we simplify the training process while negligibly increasing the inference costs. Additionally, our studies on solving multiple PDEs indicate that kernel-weighted CoRes considerably decrease the sensitivity of NNs to factors such as random initialization, architecture type, and choice of optimizer. We believe our findings have the potential to spark a renewed interest in leveraging kernel methods for solving PDEs.

GP+: A Python Library for Kernel-based learning via Gaussian Processes

In this paper we introduce GP+, an open-source library for kernel-based learning via Gaussian processes (GPs) which are powerful statistical models that are completely characterized by their parametric covariance and mean functions. GP+ is built on PyTorch and provides a user-friendly and object-oriented tool for probabilistic learning and inference. As we demonstrate with a host of examples, GP+ has a few unique advantages over other GP modeling libraries. We achieve these advantages primarily by integrating nonlinear manifold learning techniques with GPs' covariance and mean functions. As part of introducing GP+, in this paper we also make methodological contributions that (1) enable probabilistic data fusion and inverse parameter estimation, and (2) equip GPs with parsimonious parametric mean functions which span mixed feature spaces that have both categorical and quantitative variables. We demonstrate the impact of these contributions in the context of Bayesian optimization, multi-fidelity modeling, sensitivity analysis, and calibration of computer models.

Probabilistic Neural Data Fusion for Learning from an Arbitrary Number of Multi-fidelity Data Sets

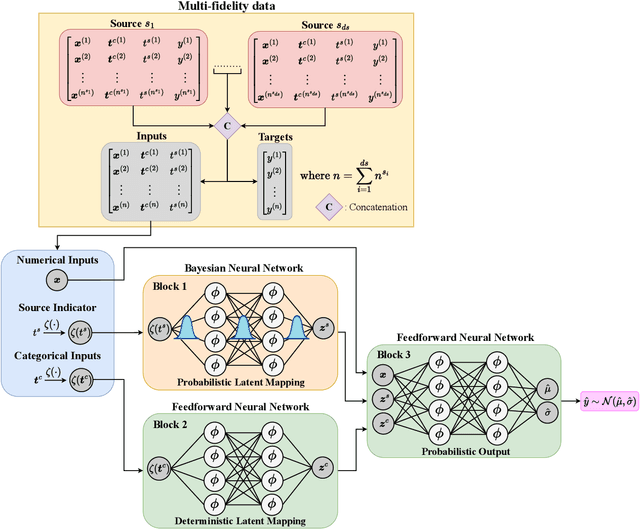
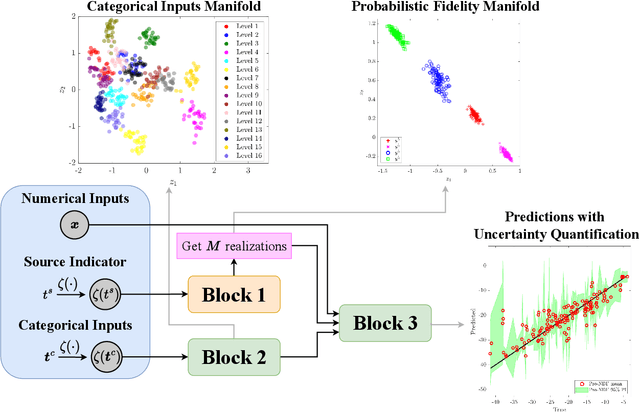
In many applications in engineering and sciences analysts have simultaneous access to multiple data sources. In such cases, the overall cost of acquiring information can be reduced via data fusion or multi-fidelity (MF) modeling where one leverages inexpensive low-fidelity (LF) sources to reduce the reliance on expensive high-fidelity (HF) data. In this paper, we employ neural networks (NNs) for data fusion in scenarios where data is very scarce and obtained from an arbitrary number of sources with varying levels of fidelity and cost. We introduce a unique NN architecture that converts MF modeling into a nonlinear manifold learning problem. Our NN architecture inversely learns non-trivial (e.g., non-additive and non-hierarchical) biases of the LF sources in an interpretable and visualizable manifold where each data source is encoded via a low-dimensional distribution. This probabilistic manifold quantifies model form uncertainties such that LF sources with small bias are encoded close to the HF source. Additionally, we endow the output of our NN with a parametric distribution not only to quantify aleatoric uncertainties, but also to reformulate the network's loss function based on strictly proper scoring rules which improve robustness and accuracy on unseen HF data. Through a set of analytic and engineering examples, we demonstrate that our approach provides a high predictive power while quantifying various sources uncertainties.