Shirin Hosseinmardi
Learning Mappings in Mesh-based Simulations
Jun 14, 2025Abstract:Many real-world physics and engineering problems arise in geometrically complex domains discretized by meshes for numerical simulations. The nodes of these potentially irregular meshes naturally form point clouds whose limited tractability poses significant challenges for learning mappings via machine learning models. To address this, we introduce a novel and parameter-free encoding scheme that aggregates footprints of points onto grid vertices and yields information-rich grid representations of the topology. Such structured representations are well-suited for standard convolution and FFT (Fast Fourier Transform) operations and enable efficient learning of mappings between encoded input-output pairs using Convolutional Neural Networks (CNNs). Specifically, we integrate our encoder with a uniquely designed UNet (E-UNet) and benchmark its performance against Fourier- and transformer-based models across diverse 2D and 3D problems where we analyze the performance in terms of predictive accuracy, data efficiency, and noise robustness. Furthermore, we highlight the versatility of our encoding scheme in various mapping tasks including recovering full point cloud responses from partial observations. Our proposed framework offers a practical alternative to both primitive and computationally intensive encoding schemes; supporting broad adoption in computational science applications involving mesh-based simulations.
Localized Physics-informed Gaussian Processes with Curriculum Training for Topology Optimization
Mar 18, 2025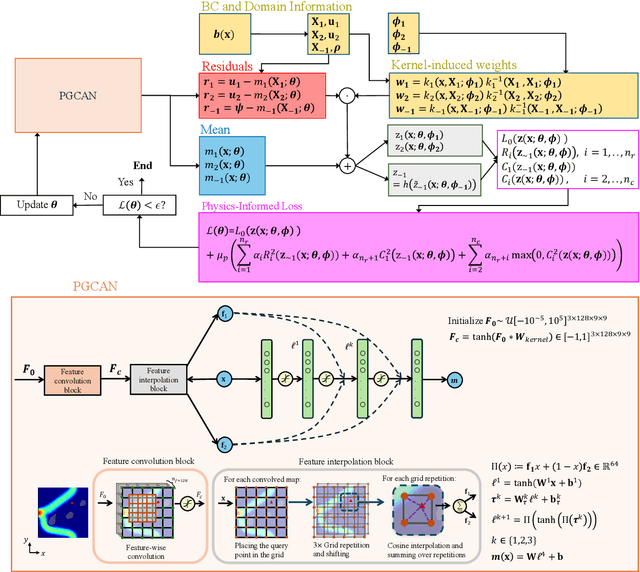
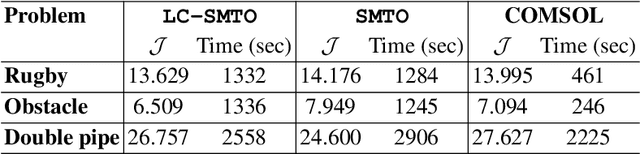
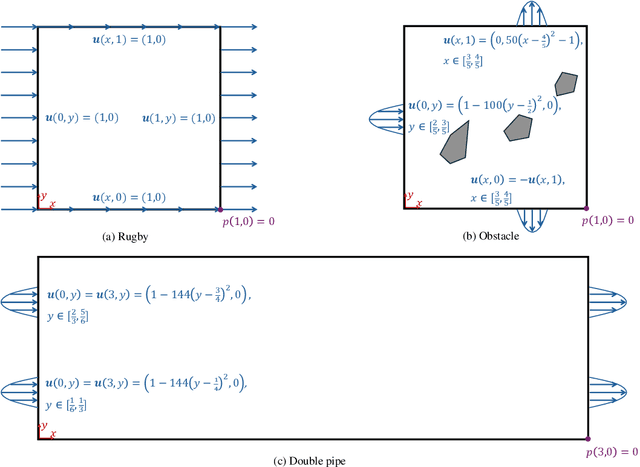
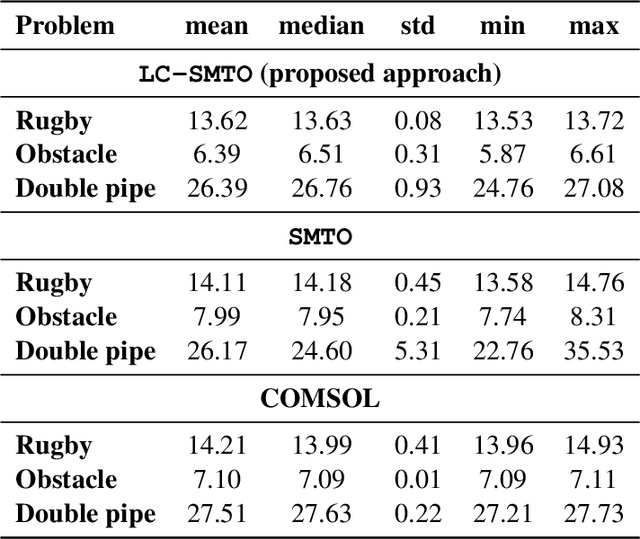
Abstract:We introduce a simultaneous and meshfree topology optimization (TO) framework based on physics-informed Gaussian processes (GPs). Our framework endows all design and state variables via GP priors which have a shared, multi-output mean function that is parametrized via a customized deep neural network (DNN). The parameters of this mean function are estimated by minimizing a multi-component loss function that depends on the performance metric, design constraints, and the residuals on the state equations. Our TO approach yields well-defined material interfaces and has a built-in continuation nature that promotes global optimality. Other unique features of our approach include (1) its customized DNN which, unlike fully connected feed-forward DNNs, has a localized learning capacity that enables capturing intricate topologies and reducing residuals in high gradient fields, (2) its loss function that leverages localized weights to promote solution accuracy around interfaces, and (3) its use of curriculum training to avoid local optimality.To demonstrate the power of our framework, we validate it against commercial TO package COMSOL on three problems involving dissipated power minimization in Stokes flow.
Operator Learning with Gaussian Processes
Sep 06, 2024


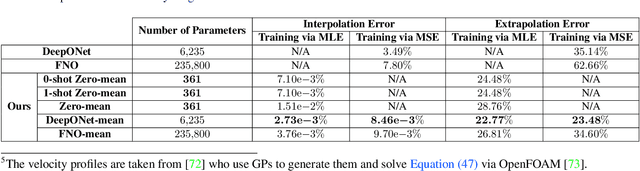
Abstract:Operator learning focuses on approximating mappings $\mathcal{G}^\dagger:\mathcal{U} \rightarrow\mathcal{V}$ between infinite-dimensional spaces of functions, such as $u: \Omega_u\rightarrow\mathbb{R}$ and $v: \Omega_v\rightarrow\mathbb{R}$. This makes it particularly suitable for solving parametric nonlinear partial differential equations (PDEs). While most machine learning methods for operator learning rely on variants of deep neural networks (NNs), recent studies have shown that Gaussian Processes (GPs) are also competitive while offering interpretability and theoretical guarantees. In this paper, we introduce a hybrid GP/NN-based framework for operator learning that leverages the strengths of both methods. Instead of approximating the function-valued operator $\mathcal{G}^\dagger$, we use a GP to approximate its associated real-valued bilinear form $\widetilde{\mathcal{G}}^\dagger: \mathcal{U}\times\mathcal{V}^*\rightarrow\mathbb{R}.$ This bilinear form is defined by $\widetilde{\mathcal{G}}^\dagger(u,\varphi) := [\varphi,\mathcal{G}^\dagger(u)],$ which allows us to recover the operator $\mathcal{G}^\dagger$ through $\mathcal{G}^\dagger(u)(y)=\widetilde{\mathcal{G}}^\dagger(u,\delta_y).$ The GP mean function can be zero or parameterized by a neural operator and for each setting we develop a robust training mechanism based on maximum likelihood estimation (MLE) that can optionally leverage the physics involved. Numerical benchmarks show that (1) it improves the performance of a base neural operator by using it as the mean function of a GP, and (2) it enables zero-shot data-driven models for accurate predictions without prior training. Our framework also handles multi-output operators where $\mathcal{G}^\dagger:\mathcal{U} \rightarrow\prod_{s=1}^S\mathcal{V}^s$, and benefits from computational speed-ups via product kernel structures and Kronecker product matrix representations.
Simultaneous and Meshfree Topology Optimization with Physics-informed Gaussian Processes
Aug 07, 2024Abstract:Topology optimization (TO) provides a principled mathematical approach for optimizing the performance of a structure by designing its material spatial distribution in a pre-defined domain and subject to a set of constraints. The majority of existing TO approaches leverage numerical solvers for design evaluations during the optimization and hence have a nested nature and rely on discretizing the design variables. Contrary to these approaches, herein we develop a new class of TO methods based on the framework of Gaussian processes (GPs) whose mean functions are parameterized via deep neural networks. Specifically, we place GP priors on all design and state variables to represent them via parameterized continuous functions. These GPs share a deep neural network as their mean function but have as many independent kernels as there are state and design variables. We estimate all the parameters of our model in a single for loop that optimizes a penalized version of the performance metric where the penalty terms correspond to the state equations and design constraints. Attractive features of our approach include $(1)$ having a built-in continuation nature since the performance metric is optimized at the same time that the state equations are solved, and $(2)$ being discretization-invariant and accommodating complex domains and topologies. To test our method against conventional TO approaches implemented in commercial software, we evaluate it on four problems involving the minimization of dissipated power in Stokes flow. The results indicate that our approach does not need filtering techniques, has consistent computational costs, and is highly robust against random initializations and problem setup.
Parametric Encoding with Attention and Convolution Mitigate Spectral Bias of Neural Partial Differential Equation Solvers
Mar 22, 2024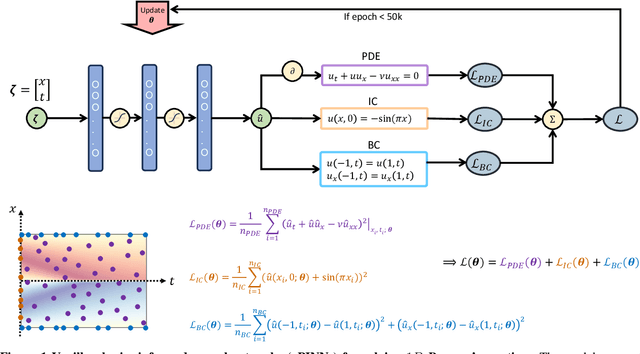
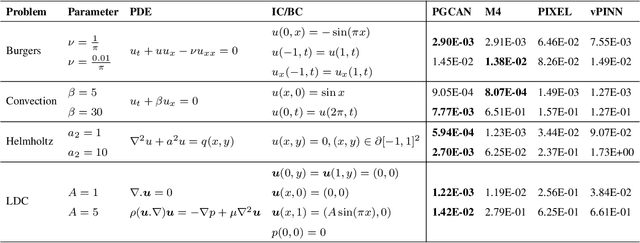
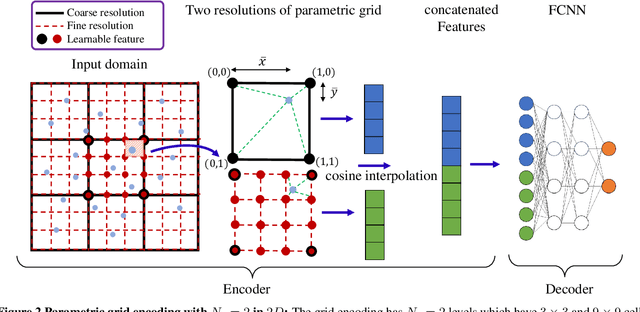
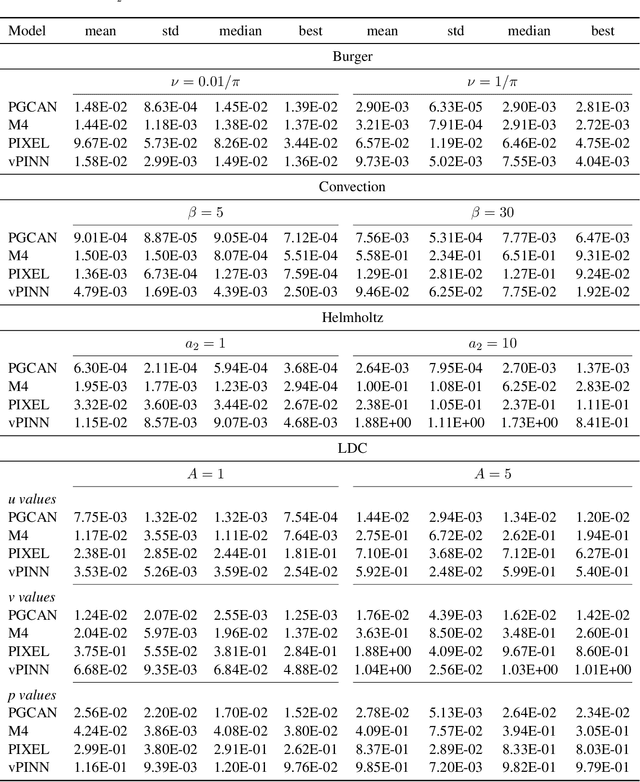
Abstract:Deep neural networks (DNNs) are increasingly used to solve partial differential equations (PDEs) that naturally arise while modeling a wide range of systems and physical phenomena. However, the accuracy of such DNNs decreases as the PDE complexity increases and they also suffer from spectral bias as they tend to learn the low-frequency solution characteristics. To address these issues, we introduce Parametric Grid Convolutional Attention Networks (PGCANs) that can solve PDE systems without leveraging any labeled data in the domain. The main idea of PGCAN is to parameterize the input space with a grid-based encoder whose parameters are connected to the output via a DNN decoder that leverages attention to prioritize feature training. Our encoder provides a localized learning ability and uses convolution layers to avoid overfitting and improve information propagation rate from the boundaries to the interior of the domain. We test the performance of PGCAN on a wide range of PDE systems and show that it effectively addresses spectral bias and provides more accurate solutions compared to competing methods.
Neural Networks with Kernel-Weighted Corrective Residuals for Solving Partial Differential Equations
Jan 07, 2024Abstract:Physics-informed machine learning (PIML) has emerged as a promising alternative to conventional numerical methods for solving partial differential equations (PDEs). PIML models are increasingly built via deep neural networks (NNs) whose architecture and training process are designed such that the network satisfies the PDE system. While such PIML models have substantially advanced over the past few years, their performance is still very sensitive to the NN's architecture and loss function. Motivated by this limitation, we introduce kernel-weighted Corrective Residuals (CoRes) to integrate the strengths of kernel methods and deep NNs for solving nonlinear PDE systems. To achieve this integration, we design a modular and robust framework which consistently outperforms competing methods in solving a broad range of benchmark problems. This performance improvement has a theoretical justification and is particularly attractive since we simplify the training process while negligibly increasing the inference costs. Additionally, our studies on solving multiple PDEs indicate that kernel-weighted CoRes considerably decrease the sensitivity of NNs to factors such as random initialization, architecture type, and choice of optimizer. We believe our findings have the potential to spark a renewed interest in leveraging kernel methods for solving PDEs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge