Parametric Encoding with Attention and Convolution Mitigate Spectral Bias of Neural Partial Differential Equation Solvers
Paper and Code
Mar 22, 2024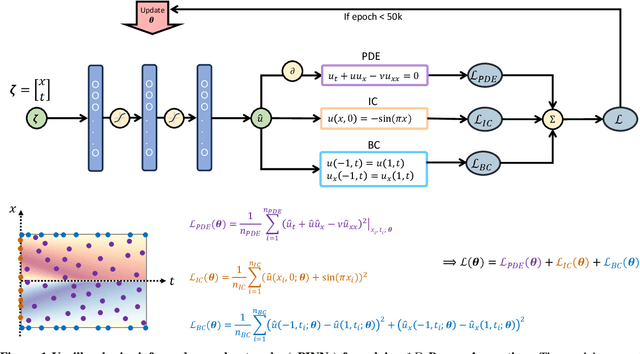
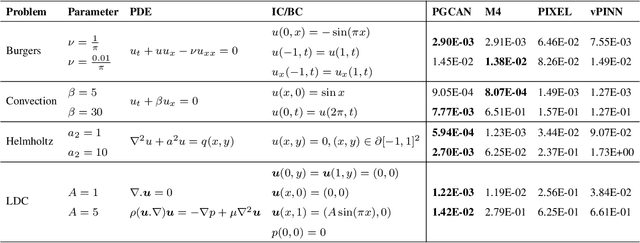
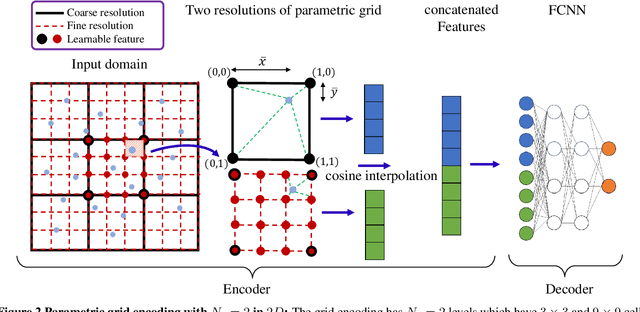
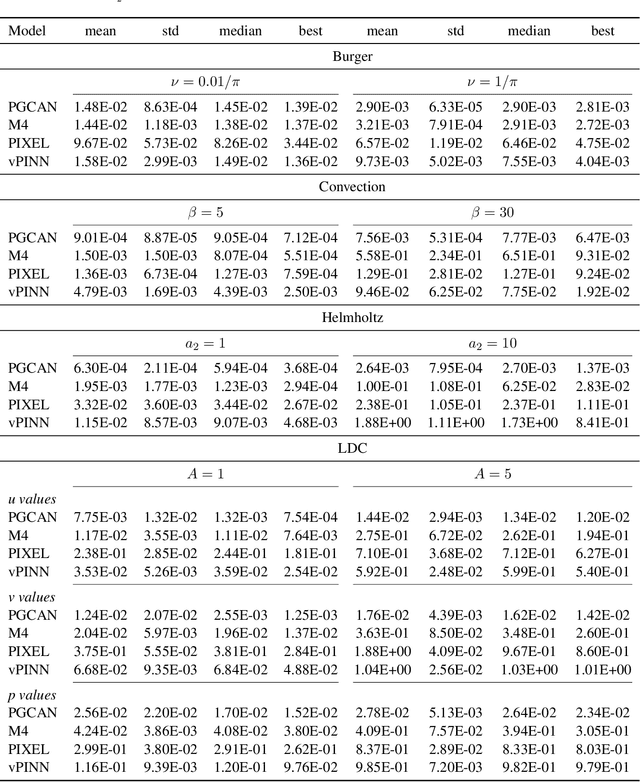
Deep neural networks (DNNs) are increasingly used to solve partial differential equations (PDEs) that naturally arise while modeling a wide range of systems and physical phenomena. However, the accuracy of such DNNs decreases as the PDE complexity increases and they also suffer from spectral bias as they tend to learn the low-frequency solution characteristics. To address these issues, we introduce Parametric Grid Convolutional Attention Networks (PGCANs) that can solve PDE systems without leveraging any labeled data in the domain. The main idea of PGCAN is to parameterize the input space with a grid-based encoder whose parameters are connected to the output via a DNN decoder that leverages attention to prioritize feature training. Our encoder provides a localized learning ability and uses convolution layers to avoid overfitting and improve information propagation rate from the boundaries to the interior of the domain. We test the performance of PGCAN on a wide range of PDE systems and show that it effectively addresses spectral bias and provides more accurate solutions compared to competing methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge