Towards Low-bit Communication for Tensor Parallel LLM Inference

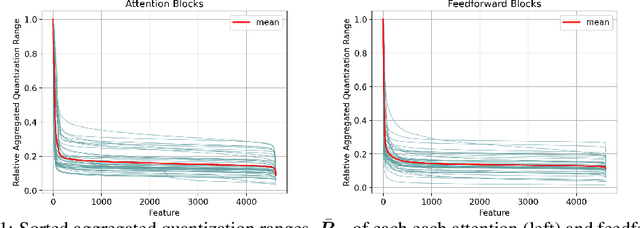
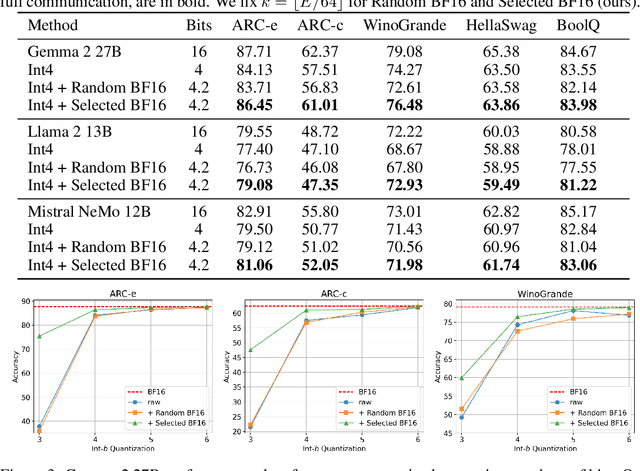
Tensor parallelism provides an effective way to increase server large language model (LLM) inference efficiency despite adding an additional communication cost. However, as server LLMs continue to scale in size, they will need to be distributed across more devices, magnifying the communication cost. One way to approach this problem is with quantization, but current methods for LLMs tend to avoid quantizing the features that tensor parallelism needs to communicate. Taking advantage of consistent outliers in communicated features, we introduce a quantization method that reduces communicated values on average from 16 bits to 4.2 bits while preserving nearly all of the original performance. For instance, our method maintains around 98.0% and 99.5% of Gemma 2 27B's and Llama 2 13B's original performance, respectively, averaged across all tasks we evaluated on.

Probabilistic Neural Data Fusion for Learning from an Arbitrary Number of Multi-fidelity Data Sets

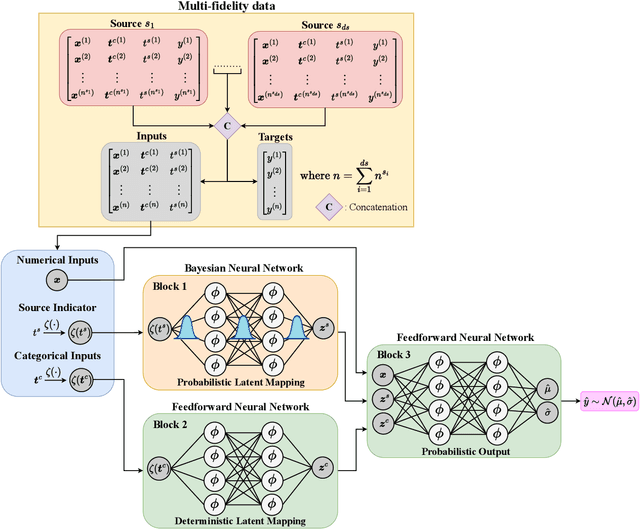
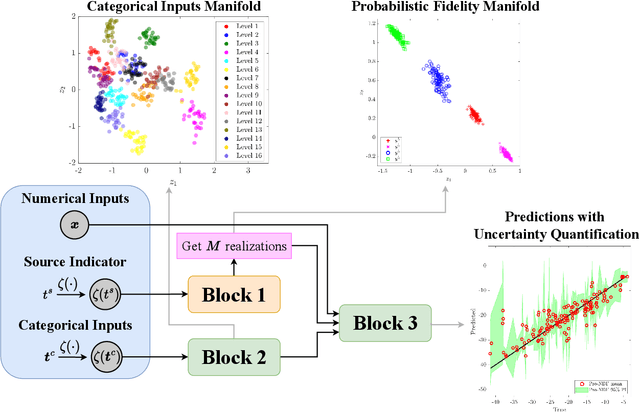
In many applications in engineering and sciences analysts have simultaneous access to multiple data sources. In such cases, the overall cost of acquiring information can be reduced via data fusion or multi-fidelity (MF) modeling where one leverages inexpensive low-fidelity (LF) sources to reduce the reliance on expensive high-fidelity (HF) data. In this paper, we employ neural networks (NNs) for data fusion in scenarios where data is very scarce and obtained from an arbitrary number of sources with varying levels of fidelity and cost. We introduce a unique NN architecture that converts MF modeling into a nonlinear manifold learning problem. Our NN architecture inversely learns non-trivial (e.g., non-additive and non-hierarchical) biases of the LF sources in an interpretable and visualizable manifold where each data source is encoded via a low-dimensional distribution. This probabilistic manifold quantifies model form uncertainties such that LF sources with small bias are encoded close to the HF source. Additionally, we endow the output of our NN with a parametric distribution not only to quantify aleatoric uncertainties, but also to reformulate the network's loss function based on strictly proper scoring rules which improve robustness and accuracy on unseen HF data. Through a set of analytic and engineering examples, we demonstrate that our approach provides a high predictive power while quantifying various sources uncertainties.