Probabilistic Neural Data Fusion for Learning from an Arbitrary Number of Multi-fidelity Data Sets

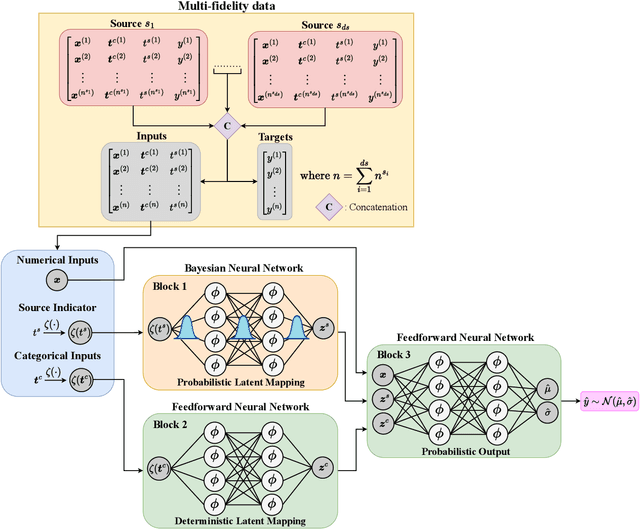
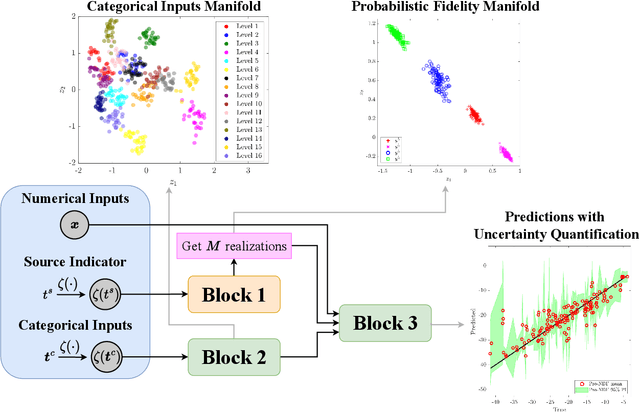
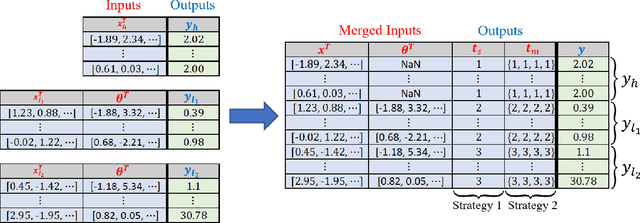
In many applications in engineering and sciences analysts have simultaneous access to multiple data sources. In such cases, the overall cost of acquiring information can be reduced via data fusion or multi-fidelity (MF) modeling where one leverages inexpensive low-fidelity (LF) sources to reduce the reliance on expensive high-fidelity (HF) data. In this paper, we employ neural networks (NNs) for data fusion in scenarios where data is very scarce and obtained from an arbitrary number of sources with varying levels of fidelity and cost. We introduce a unique NN architecture that converts MF modeling into a nonlinear manifold learning problem. Our NN architecture inversely learns non-trivial (e.g., non-additive and non-hierarchical) biases of the LF sources in an interpretable and visualizable manifold where each data source is encoded via a low-dimensional distribution. This probabilistic manifold quantifies model form uncertainties such that LF sources with small bias are encoded close to the HF source. Additionally, we endow the output of our NN with a parametric distribution not only to quantify aleatoric uncertainties, but also to reformulate the network's loss function based on strictly proper scoring rules which improve robustness and accuracy on unseen HF data. Through a set of analytic and engineering examples, we demonstrate that our approach provides a high predictive power while quantifying various sources uncertainties.

Data Fusion with Latent Map Gaussian Processes

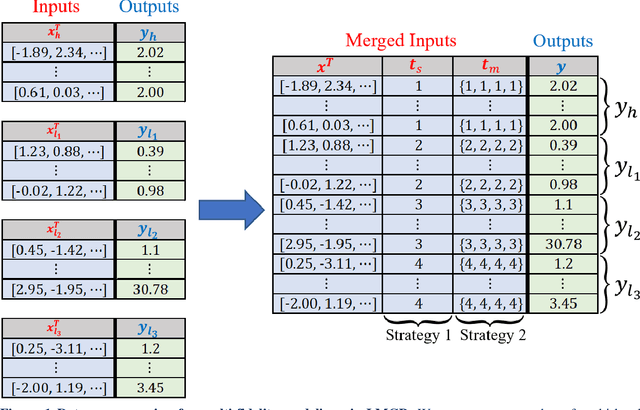
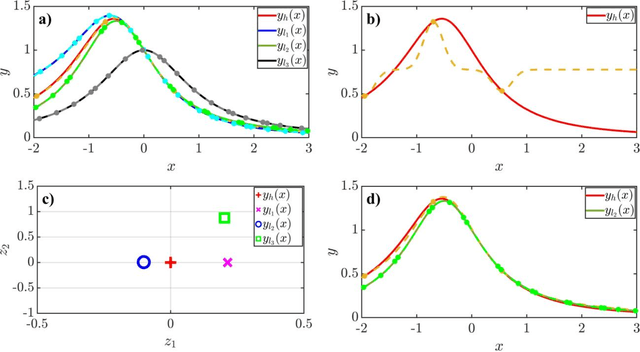
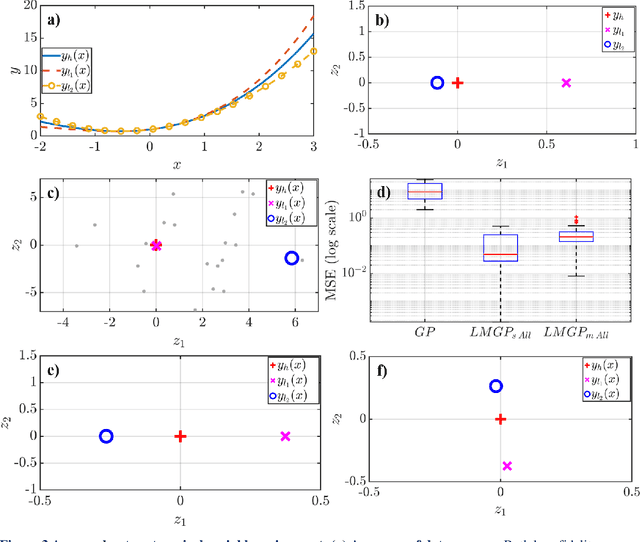
Multi-fidelity modeling and calibration are data fusion tasks that ubiquitously arise in engineering design. In this paper, we introduce a novel approach based on latent-map Gaussian processes (LMGPs) that enables efficient and accurate data fusion. In our approach, we convert data fusion into a latent space learning problem where the relations among different data sources are automatically learned. This conversion endows our approach with attractive advantages such as increased accuracy, reduced costs, flexibility to jointly fuse any number of data sources, and ability to visualize correlations between data sources. This visualization allows the user to detect model form errors or determine the optimum strategy for high-fidelity emulation by fitting LMGP only to the subset of the data sources that are well-correlated. We also develop a new kernel function that enables LMGPs to not only build a probabilistic multi-fidelity surrogate but also estimate calibration parameters with high accuracy and consistency. The implementation and use of our approach are considerably simpler and less prone to numerical issues compared to existing technologies. We demonstrate the benefits of LMGP-based data fusion by comparing its performance against competing methods on a wide range of examples.