Data Fusion with Latent Map Gaussian Processes

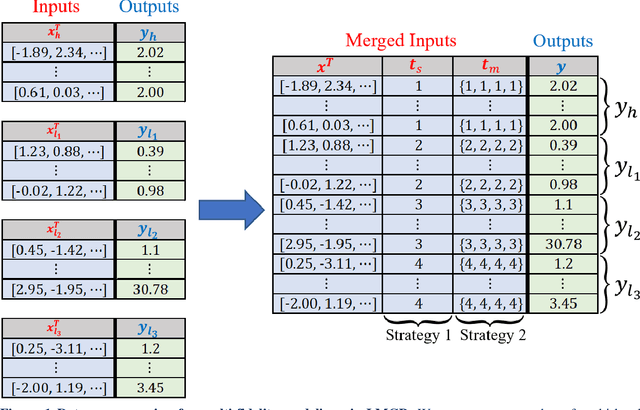
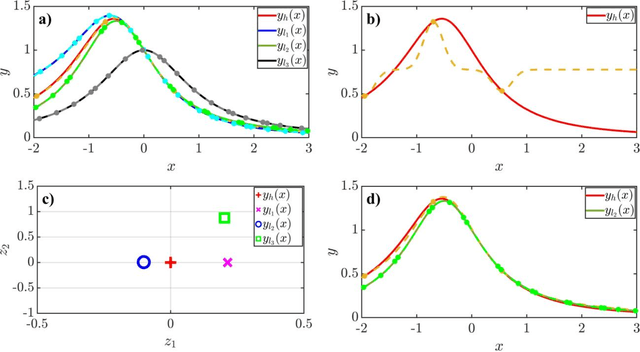
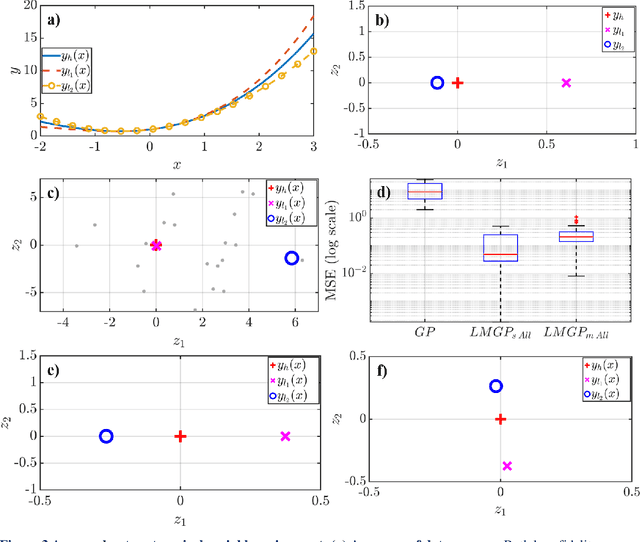
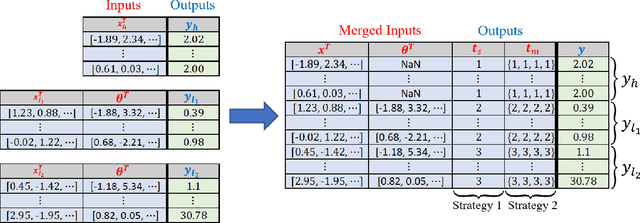
Multi-fidelity modeling and calibration are data fusion tasks that ubiquitously arise in engineering design. In this paper, we introduce a novel approach based on latent-map Gaussian processes (LMGPs) that enables efficient and accurate data fusion. In our approach, we convert data fusion into a latent space learning problem where the relations among different data sources are automatically learned. This conversion endows our approach with attractive advantages such as increased accuracy, reduced costs, flexibility to jointly fuse any number of data sources, and ability to visualize correlations between data sources. This visualization allows the user to detect model form errors or determine the optimum strategy for high-fidelity emulation by fitting LMGP only to the subset of the data sources that are well-correlated. We also develop a new kernel function that enables LMGPs to not only build a probabilistic multi-fidelity surrogate but also estimate calibration parameters with high accuracy and consistency. The implementation and use of our approach are considerably simpler and less prone to numerical issues compared to existing technologies. We demonstrate the benefits of LMGP-based data fusion by comparing its performance against competing methods on a wide range of examples.

Latent Map Gaussian Processes for Mixed Variable Metamodeling

Gaussian processes (GPs) are ubiquitously used in sciences and engineering as metamodels. Standard GPs, however, can only handle numerical or quantitative variables. In this paper, we introduce latent map Gaussian processes (LMGPs) that inherit the attractive properties of GPs but are also applicable to mixed data that have both quantitative and qualitative inputs. The core idea behind LMGPs is to learn a low-dimensional manifold where all qualitative inputs are represented by some quantitative features. To learn this manifold, we first assign a unique prior vector representation to each combination of qualitative inputs. We then use a linear map to project these priors on a manifold that characterizes the posterior representations. As the posteriors are quantitative, they can be straightforwardly used in any standard correlation function such as the Gaussian. Hence, the optimal map and the corresponding manifold can be efficiently learned by maximizing the Gaussian likelihood function. Through a wide range of analytical and real-world examples, we demonstrate the advantages of LMGPs over state-of-the-art methods in terms of accuracy and versatility. In particular, we show that LMGPs can handle variable-length inputs and provide insights into how qualitative inputs affect the response or interact with each other. We also provide a neural network interpretation of LMGPs and study the effect of prior latent representations on their performance.