Scrutinizing the Vulnerability of Decentralized Learning to Membership Inference Attacks

The primary promise of decentralized learning is to allow users to engage in the training of machine learning models in a collaborative manner while keeping their data on their premises and without relying on any central entity. However, this paradigm necessitates the exchange of model parameters or gradients between peers. Such exchanges can be exploited to infer sensitive information about training data, which is achieved through privacy attacks (e.g Membership Inference Attacks -- MIA). In order to devise effective defense mechanisms, it is important to understand the factors that increase/reduce the vulnerability of a given decentralized learning architecture to MIA. In this study, we extensively explore the vulnerability to MIA of various decentralized learning architectures by varying the graph structure (e.g number of neighbors), the graph dynamics, and the aggregation strategy, across diverse datasets and data distributions. Our key finding, which to the best of our knowledge we are the first to report, is that the vulnerability to MIA is heavily correlated to (i) the local model mixing strategy performed by each node upon reception of models from neighboring nodes and (ii) the global mixing properties of the communication graph. We illustrate these results experimentally using four datasets and by theoretically analyzing the mixing properties of various decentralized architectures. Our paper draws a set of lessons learned for devising decentralized learning systems that reduce by design the vulnerability to MIA.

Differentially private and decentralized randomized power method

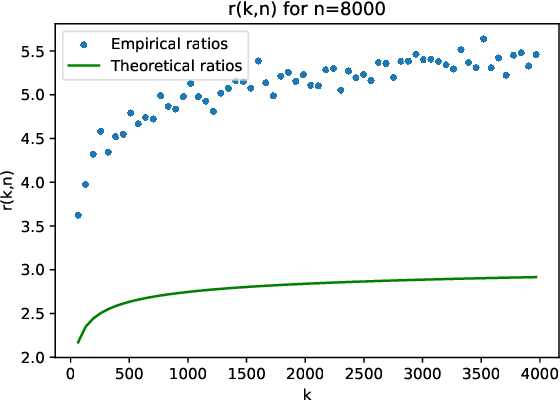
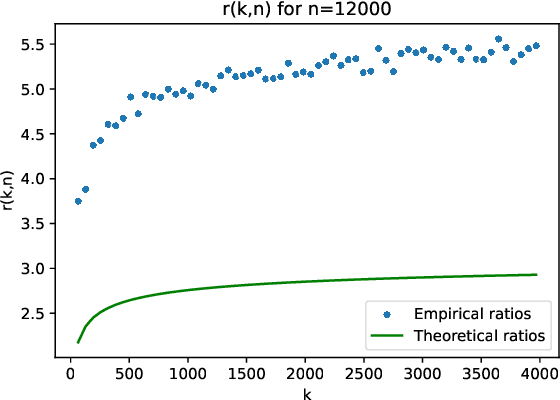
The randomized power method has gained significant interest due to its simplicity and efficient handling of large-scale spectral analysis and recommendation tasks. As modern datasets contain sensitive private information, we need to give formal guarantees on the possible privacy leaks caused by this method. This paper focuses on enhancing privacy preserving variants of the method. We propose a strategy to reduce the variance of the noise introduced to achieve Differential Privacy (DP). We also adapt the method to a decentralized framework with a low computational and communication overhead, while preserving the accuracy. We leverage Secure Aggregation (a form of Multi-Party Computation) to allow the algorithm to perform computations using data distributed among multiple users or devices, without revealing individual data. We show that it is possible to use a noise scale in the decentralized setting that is similar to the one in the centralized setting. We improve upon existing convergence bounds for both the centralized and decentralized versions. The proposed method is especially relevant for decentralized applications such as distributed recommender systems, where privacy concerns are paramount.

Distributed Differentially Private Averaging with Improved Utility and Robustness to Malicious Parties

Learning from data owned by several parties, as in federated learning, raises challenges regarding the privacy guarantees provided to participants and the correctness of the computation in the presence of malicious parties. We tackle these challenges in the context of distributed averaging, an essential building block of distributed and federated learning. Our first contribution is a novel distributed differentially private protocol which naturally scales with the number of parties. The key idea underlying our protocol is to exchange correlated Gaussian noise along the edges of a network graph, complemented by independent noise added by each party. We analyze the differential privacy guarantees of our protocol and the impact of the graph topology, showing that we can match the accuracy of the trusted curator model even when each party communicates with only a logarithmic number of other parties chosen at random. This is in contrast with protocols in the local model of privacy (with lower accuracy) or based on secure aggregation (where all pairs of users need to exchange messages). Our second contribution is to enable users to prove the correctness of their computations without compromising the efficiency and privacy guarantees of the protocol. Our construction relies on standard cryptographic primitives like commitment schemes and zero knowledge proofs.